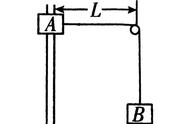
如下是一个反比例函数图形,我们在初中就已经很熟悉的,它的主要特点是:如果用几何图形表示,假设它的宽度是X时,高度就必须是1/X,所以它的总面积永远是1,根据这个结论我们就可以用几何原理来分析它的导数原理

首先,当x变化,为了保持总面积等于1,对应的1/x就要作相应的变化,所以当X的微小增量是dx时,图形右边增加了一个新的面积区域,那么对应的高度就要降低d(1/x)

这样顶部减少的面积就等于右边增加的面积, 这时的d(1/x)是一个负值,因为它减少了长方形的高度

那么它的导数怎么计算的,这个思路很完美

所以根据上述两个面积相等,得到一个如下形式的等式,注意这里的d(1/x)是一个负值,所以得到

这就是反比例函数的导数原理,非常有趣
,