众所周知,微积分是现代科学的基础。正是有了微积分之后,我们才有了研究万物变化的数学工具。举个最简单的例子:位移对时间的一阶导数代表位移的变化率,也就是速度;位移对时间的二阶导数代表速度的变化率,即加速度;等等。反过来,加速度对时间的一阶积分是速度,二阶积分是位移。
但是,不知你注意到了没有:不论求导也好,积分也好,传统的微积分都是整数阶的,有没有分数阶的呢?譬如,能不能对位移求1/2阶导数呢?
事实上,早在300多年前就有人向微积分的发明人之一(另一位发明人是牛顿)德国数学家莱布尼兹请教过这个问题。当时,可把这位数学大师问哑了。是啊,分数阶导数是什么意思呢?又该怎么去操作呢?这真是难以想象。
然而,今天,数学家对此问题不仅给出了肯定的回答,还发展出一门在现实中有着广泛应用的新的数学分支——分数微积分。
如何对函数进行分数阶求导?
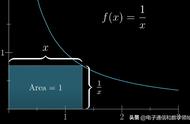
我相信,当你读到这里,一定急于知道分数阶的微分和积分是如何操作的。让我们先来看一个简单的幂函数f'(x)=xn,其中n为整数。
我们知道,对它进行一阶求导,有f'(x)=nxn-1,对它进行二阶求导,有f''(x)=n(n-1)Xn-2,以此类推,对它进行k阶求导,有

其中n!=1×2×3×……×n。
为方便起见,我们定义一个Γ函数,Γ(m)=(m-1)!
这样,上面式子可改写为

在传统微积分中,k是整数,我们现在要把它推广到分数。但Γ函数中的自变量只能取整数,譬如Γ(1/2)是没有意义的,为了让Γ函数在自变量为分数的情况下也有意义,我们需要先将它进行推广,让它在自变量为分数时也有意义。
如何推广呢?我们注意到Γ函数有个特点,即