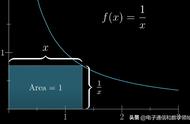
因为任何连续函数原则上都能展开成幂函数的无穷级数求和的形式,所以知道了如何对幂函数分数阶求导,理论上你也就能对任何连续函数进行分数阶求导。
揭示大自然更复杂的细节
知道了分数微积分如何计算之后,想必你又要问:分数微积分代表什么意思呢?
这个问题不好回答。整数阶的导数相对还比较直观,譬如位移对时间的一阶导数是速度,位移对时间的二阶导数是加速度……但位移对时间的1/2阶导数是什么意思,还真答不上来,因为现实中并没有一个直观的对应物。我们不妨只把分数微积分当作一项数学工具,是对传统微积分的一个微调。
怎么理解后面这一点呢?
举例来说。你可以用一阶微分来模拟粘性液体的运动,因为液体的粘性通常与运动速度有关。同样,你也可以用二阶微分来模拟有弹性的固体(比如弹簧)的运动,因为它们的弹性通常与加速度有关。然而,自然界中还存在大量介于两者之间的材料,比如我们身上的动脉壁,它们既有点像粘性的液体,又有点像有弹性的固体。一阶微分和二阶微分都不适合给它们建立准确的数学模型。这个时候,我们就要求助于分数阶的微积分了。
总之,我们使用数学是试图捕捉和理解自然,但自然是复杂的,而分数微积分能允许我们比传统微积分更精确地揭示大自然的复杂细节。
目前,从研究癌细胞扩散到药物输送,再到制造更高效的电池,分数微积分已经获得了广泛的应用。
,