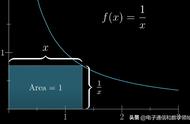
数学家发现,有这样的一个连续函数,也满足

这个条件。这个函数是以积分形式出现的:

你可能不太习惯这种形式的函数,但事实上,在这个积分中变量x被积分掉了,最后的结果只跟z有关,所以这是一个关于z的函数,其中z为任意大于零的实数。
于是,当Γ函数的自变量为分数时,只需代入上式,就可以计算出来结果。这样一来,幂函数的分数阶导数也就可以计算了。
现在,让我们来演示一下如何对f(x)=x进行1/2阶求导。这里,n=1,k=1/2。我们有

这就是对函数f(x)=x进行1/2阶求导的结果。
我们知道,连续两次1/2阶求导应该等于一次一阶求导。是不是这样呢?我们不妨f(x)=x拿验证一下。大家知道,对它一阶求导结果是1。你不妨对上式再进行一次1/2阶求导,你会发现结果确实是1。