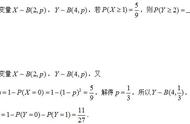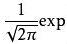对于需要统计的一组数据,高一学生学完了代表集中趋势的中位数、众数、平均数之后,就会学到衡量数据离散程度的数字特征——方差,描述的是这一组数据与平均数的平均偏离程度,当然描述部分数据的偏离程度还有极差,消除单位影响之后还有标准差,这里咱们把目光暂时集中在方差上,另外用样本估计总体就不说了。
方差顾名思义,有平方、有作差,这个名字已经显现了方差的计算方法和计算公式的一部分,加上“平均偏离程度”,就有1/n,这样就完整了。
从教材内容来看,是以选择甲乙两个运动员谁去参赛作为问题背景的:均值相同的情况,谁的方差小,谁的成绩就更稳定,也就更容易在大赛打出相对较好的成绩。从生活实际来说,这个道理不难理解,但是要彻底弄懂方差的概念、公式,还需要问自己如下几个问题:
1、结合教材在引入方差这个概念之前,对于射击这个的问题情境,教材给的是2个独立的条形图,能不能引导学生来整理为更易于理解的形式呢?

在课堂上,对于射击问题,先让学生们自由讨论,畅所欲言2分钟,再反问那些答对的同学:你是凭感觉还是靠的逻辑证明?再引导学生,请2名同学一起合作把上图画出来,然后再让大家通过两个目标对象合在一起的二维折线图直观说明,确实乙运动员的成绩更加稳定,接着引入为方差作铺垫的“平均距离”。
第一步,x1-x拔,x2-x拔,……,xn-x拔
到n说明是有限个数据,高中阶段暂时处理这么多。大家会发现作差后新产生的n个数据有正有负,而从黑板上的图来观察,距离要加总的,因此每个数据都得是非负数,比如加绝对值,要不然正负抵消,失去评估数据波动幅度的意义;
第二步,加了绝对值后也能手工计算,但是数据量大且多的时候,使用计算机遇到绝对值机械式分类讨论不聪明,于是采用人工和计算机都好处理的平方和运算,顺便把差的值同时做大,也更容易比较两者之间的波动幅度;
第三步,除以n,给平均一个交待,大家也会发现要比较2个或多个数据的方差,它们的样本容量肯定要一样,否则不公平。
2、为什么要用每个具体数据xi跟平均数x拔做对比呢?难道不能让所有的数据跟第一个数或者中位数进行作差平方和再均值的计算吗?
这里面到底有什么“道道”?请看下面2个实例:
例1:求绝对值函数y=f(x)=|x-a| |x-b|(x∈R,a≠b)的最小值。
在数轴上画出来,一眼可知最小值就是a到b的距离,即|a-b|,取得最小值的条件就是x要在a和b之间;
例2:求二次函数y=g(x)=(x-a)^2 (x-b)^2(x∈R,a≠b)的最小值。
画出二次函数的草图,开口向上,最小值在对称轴x=(a b)/2处取得;
把例1和例2联系在一起看,求方差为什么都要减去x拔的价值不言自明:就是要让方差的数值尽可能小,小小益善不是吗?
方差不仅仅是偏离程度的平均值,而且是可以计算得到的最小值,这和高二线性回归分析中求斜率参数b尖(帽)的最小二乘法的思路是一致的,高一这一节
方差概念的教学可以作为最小二乘法得到线性回归方程中斜率参数的前奏。
其实,现实中很多东西并非十分精确的、也难以做到无误,但是为了数学化,就用一个可测度的值来替代,包括概率也是这么回事。
3、方差的基础是这一组数据的平均数,进一步说,两组数据如果平均数不一样,那么比较方差就没有基础,也就无从比较起;
进一步想想,如果两者均值不一样,一个均值大、一个均值小,一个方差大、一个方差小,如何比较呢,咱们分类讨论瞧瞧:

对于情况1和4的分析,第三个细分情况
类似于正态分布的3σ区间,都是采用了区间判断的方法,
根据甲乙两人的射击数据,谁更多地、概率更大地落在赛前制定的成绩区间,就派谁去,把离散的数据点变为连续的数据区间。
最后总结一下,高中阶段许多知识点间有直接或间接的联系,联系是普遍的;少一些的知识点也少不了对立和矛盾,做对看情况。因此,对于某一个具体的知识点,经常提问题、问十个为什么,把其他学过的知识点进行联系和对比总会有一些新的收获,毕竟教材不是面面俱到的高中数学百科全书。
本文表述不太严谨,上课应以教材和教参为准,平时表述思想略随意,借康托尔大师的话给自己找个台阶哈——数学的本质在于它的自由。