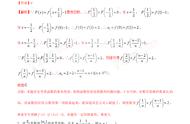前几期我们都有讲到与数列相关的高考数学试题,有读者私信本人,希望讲讲数列求和类问题,那么我们今天就讲讲怎么化解数列求和类问题。
数列求和相关知识内容,可以说是数列的核心与基础,只要跟数列相关的数学问题,都会牵扯到数列求和问题。
在高考中,数列求和问题大部分情况下都会与函数、不等式、三角、几何等知识结合,重点考查分组求和、拆项相消、错位相减等求和方法,常以小题或大题的一问的形式出现,有一定的难度。
那么在高考数学中有哪些数列求和的方法?
1、公式法
如果一个数列是等差数列或等比数列,则求和时直接利用等差、等比数列的前n项和公式,注意等比数列公比q的取值情况要分q=1或q≠1.
一些常见数列的前n项和公式:
(1)1+2+3+4+…+n=n(n 1)/2;
(2)1+3+5+7+…+2n-1=n2;
(3)2+4+6+8+…+2n=n2+n.
2、倒序相加法
如果一个数列{an},首末两端等“距离”的两项的和相等或等于同一常数,那么求这个数列的前n项和即可用倒序相加法,等差数列的前n项和即是用此法推导的。

3、分组转化求和法
若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组转化法,分别求和而后相加减。
若给出的数列不是特殊数列,但把数列的每一项分成两项,或把数列的项重新组合,使之转化为特殊数列,再利用特殊数列的前n和公式求前n项和。
4、错位相减法
如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和即可用此法来求,等比数列的前n项和就是用此法推导的。
5、裂项相消法
把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和。
典型例题分析1:
已知递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=anlog1/2an,Sn=b1+b2+…+bn,求Sn.
解:(1)设等比数列{an}的首项为a1,公比为q.
依题意,有2(a3+2)=a2+a4,
代入a2+a3+a4=28,得a3=8.
∴a2+a4=20.


数列作为高考数学的重难点,除了考查大家对数列基础知识掌握程度之外,更加考查大家运用知识解决问题能力水平的高低,如在复杂的综合问题或压轴题当中,我们要学会抓住数列这个突破口,切入问题的要害所在,抓住问题的关键。
具体来说,一般的数列求和,应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为与特殊数列有关或具备某种方法适用特点的形式,从而选择合适的方法求和。
同时解决非等差、等比数列的求和,主要有两种思路:
1、转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成。
2、不能转化为等差或等比数列的数列,往往通过裂项相消法、错位相减法、倒序相加法等来求和。
典型例题分析2:
已知等差数列{an}满足:a5=9,a2+a6=14.
(1)求{an}的通项公式;
(2)若bn=an+qan(q>0),求数列{bn}的前n项和Sn.

若数列中的每一项都可分成两项的差,求和时中间的一些项正好相互抵消,于是将前n项和转化为首尾若干项和,常用裂项消去法.常用的拆项公式有:

用错位相减法求和应注意:
1、要善于识别题目类型,特别是等比数列公比为负数的情形;
2、在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式。
在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解。
对等比数列与等差数列对应项乘积构成的新数列的求和问题,常用错位相减法,即两边同乘以等比数列的公比,然后前后两个和式错位相减即合并同类相,化为等比数列求和问题,用等比数列求和公式求和,注意第一个和式的第一项与第二和式的最后一项相减时符号变化,求和时注意够成等比数列第一项与项数及不构成等比的几项,结果要化为最简形式。
,