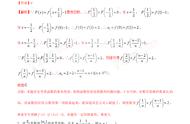等差数列是我们小学必须要掌握的基础知识,在小升初考试多以填空题、计算题的形式出现,并且在初、高中的学习过程中也会经常遇见它,现在就让我们一起来学习一下吧!
知识点:
1.把若干个数排成一列叫数列,其中每一个数都称为一项,排在第一个位置的叫首项,排在最后一个位置的叫末项,从第二项起,后项与前项的差都相等的数列叫等差数列,相邻两项的差叫做等差数列的公差,数列中数的个数叫公差。
2.通项公式:末项=首项 (项数-1)x公差
项数公式:项数=(末项-首项)÷公差 1
求和公式:总和=(首项 末项)x项数÷2

例题:
若干人围成8圈,一圈套一圈,从外向内各圈人数依次少4人,如果共有304人,最外圈有几人?
分析:根据题目可看成这是一个公差为4,项数为8,总和为304的等差数列,求末项值,根据公式末项=首项 (项数-1)x公差,可计算出末项(最外圈人数),再根据公式总和=(首项 末项)x项数÷2 即可计算出结果,为方便计算,设首项为a1。
解:设首项为a1
最外圈人数:a1 (8-1)x4=a1 28
304=(a1 a1 28)x8÷2
2a1 28=76
a1=24
24 28=52(人)
答:最外圈有52人。
等差数列总结
一通项公式
通项公式:an=a1 (n-1)·d
推论:an=am (n-m)·d ,其中am表示为第m项
备注:
等差数列的通项,整理后为类似一次函数“an=kn b”形式,其中等差数列的公差d为k。另外凡是一个数列的通项可以写成类似一次函数 “an=kn b”的形式,那么这个数列一定是等差数列。
二求和公式
Sn=na1 n(n-1)/2,这个公式通常在解答题运用比较多
Sn=n(a1 an)/2,这个公式通常在选择、填空运用比较多
备注:
1.等差数列的前n项和公式,整理后为类似二次函数“Sn=An2 Bn (常数项为0)”形式,其中等差数列的公差d为2A。另外凡是一个数列的通项可以写成类似二次函数“Sn=An2 Bn(常数项为0)”形式,那么这个数列一定是等差数列。
2. 针对等差数列,无论题目中给出何种条件的等式,最终均可以根据公式化成只有a1跟d两个未知量,从而进行求解。
三等差中项
如果2m=p q,则2am=ap aq
备注:
题目中如果给出三项的和,通常都可求出中间项为多少。例如已知等差数列a1 a2 a3=9,即可知a2=3,因为a2是a1跟a3的中间项;再如已知等差数列a1 a5 a9=12,即可知a5=4,因为a5是a1跟a9的中间项
例题:
数列{an}是等差数列,已知a5=3,求S9=?
解析:
S9=a1 a2 a3 a4 a5 a6 a7 a8 a9,可以发现a5是a1和a9,a2和a8,a3和a7,a4跟a6的中间项,即2a5=a1 a9,剩下的同理,所以S9=9a5=27
变式:
数列{an}是等差数列,前3项的和为6,后3项的和为18,Sn=128,求n
备注:
当n为奇数,

,其中

为Sn的中间项。
例如:n=11 ,S11=11a6,a6是S11的中间项。
当n为偶数,