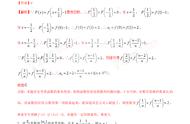3.如果{an}是等差数列,公差为d,每隔k项之后(am,am k,am 2k,am 3k ……) 也是等差数列,公差为k·d
4.如果{an}是等差数列,公差为d,数列总共有2n(偶数)项,奇数项有n个,偶数项有n个,那么

其中an跟an 1是这个数列(总共有2n项)的中间两项,因为数列的总项数是偶数的,所以才有中间两项,另S偶-S奇=nd;如果数列总共2n 1(奇数)项,奇数项有n 1个,偶数项有n个,那么

其中an 1是这个数列(总共有2n 1项)的中间项,因为数列的总项数是奇数的,所以中间只有一项。另S奇-S偶=an 1。
例题:
已知{an}是等差数列,当n=25时,奇数项的和与偶数项的和之比是多少
解析:
根据上式可知,如果数列为奇数项,所以

,已知2n 1=25,则n=12,则