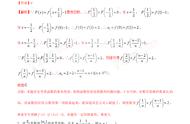一、等差数列
设等差数列{an}的公差为d
通项公式:an=a1 (n-1)d(n≥2)
前n项和为:Sn=na1 n(n-1)d/2
=(a1 an)n/2
当n为奇数时候:Sn=n*中间项
当n为偶数时候:Sn=n*中间两项和/2
特殊性质:当m n=p q时,则am an=ap aq。
二、等比数列
设等比数列{an}的公比为q
则通项公式为:an=a1qn-1(n≥2)
那么Sn=a1 a2 a3 …… an
=a1 a1q a1q2 …… a1qn-1………(1)
对(1)式两边同时乘q得
qSn= a1q a1q2 a1q3 …… a1qn-1 a1qn…(2)
当q≠1时,由(1)—(2)得
(1-q)Sn= a1- a1qn=a1(1-qn)
当q=1时,
Sn=a1 a2 a3 …… an=a1 a1 a1 …… a1=na1
∴等比数列的前n项和公式为
当q≠1时,Sn=a1(1-qn)/(1-q)
当q=1时 ,Sn=na1
特殊性质:当m n=p q时,则am*an=ap*aq。
,