【导读】
小编为帮助各位考生顺利通过事业单位招聘考试!今天为大家带来数量关系解题技巧:比例—比例巧解方程。
在数学板块中常用方法之一的比例法,是公职和各大的考试和多数考生易使用到的一个方法,主要涉及利润问题、行程和工程中,在通过设未知数列方程时普遍使用传统的方法算出结果。但实际会发现在一些涉及比例的题目中我们通过比例的性质来解方程会更简单。
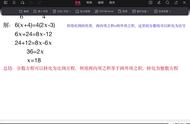
例1、(18-X)/(15-X)=4/3这道题目可以通过传统方法两个分数相等交叉相乘相等来解题。我们来观察这两个分数的特点18-X和15-X实质上的差额是不变的为3,而对应的4/3(4:3)的差额为1。按照比例的对应根据实际的差找比例对应的差差额1→3,则4→12,3→9

18-X=12,X=6
例2、½(x-1) 1=¾(x-3),对于这类题目我们可以先看作½(x 1)=¾(x-3),相当于是甲=(x 1),乙=(x-3)。甲:乙=6:4比值差2,对应实差量为(x 1)和(x-3)的差为4,既2→4,则6→3,4→2,x=11

应用-牛吃草问题
例1、 现有一块草地供牛吃,如果供27头牛可以吃6天,23头牛可以吃9天,那么21头牛可以吃多少天?
解析:根据牛吃草的公式可以列出方程(27-x)6=(23-x)9=(21-x)T根据比例思想解方程,我们不需要求x为多少,只需要计算出最后的T就行。27-x:23-x=9:6, 两者最简比3;2,差1→4,则23-x=8,23-x比21-x大2,21-x=6。 (23-x)9=72=(21-x)T =6T,得到T=12。
,