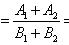有关比例的求值问题,常常可以用下面的四种方法来处理:
(1) 运用比例的性质
对已知的等式,利用比例的性质,如比例的基本性质、合比性质、等比性质进行变换,求出所求式子的值;
(2) 代入消元法
在求一个比的值时,可根据已知等式,用一个字母表示其它字母,并代入所求的比中,使比的前项、后项都用同一个字母表示,整理后约去这个字母,求出其比的值;
(3) 等比设值法
对于有等比条件求比值的题目,可设等比为K,把每个比的前项用K与比的后项的积表示,将其代入所求式中,求出其值;
(4) 特殊值法
对于求比值的填空题,选择题,选取满足已知条件的值,代入所求式中,求出其值。
下面举例说明:
例1、 若4:(a 2)=3:(2a 1),求a的值.
【解】由比例的基本性质,可得:4(2a 1)=3(a 2)解得a=2/5.
【点评】本题根据比例的基本性质,将比例式化成关于a的一元一次方程,解这个一元一次方程,求出a的值.
例2、若(x-y):y=1:2,则x:y=_____________.

例3、若a:b=c:d=e:f=2:3,则(a-2c 3e):(b-2d 3f)=______.

【点评】解法一是利用等比性质求解的,解题过程比较简捷,对于所求比中对应项字母系数相同时,宜采用等比性质来求;解法二是运用等比设值法求解的,其中k=2/3.
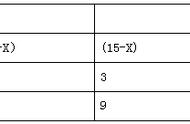
例4、若x:2=y:5=z:7,则(x-2y 3z):(x-4y 5z)=______.

【点评】本题也可以利用等比性质来解,但比较繁杂,而用等比设值法来求就比较简捷。因此,在解等比条件求值问题时,宜采用等比设值法求解,另外,对等比条件的证明题,运用等比设值法往往可获得巧解。
例5、若x=a:(b c)=b:(c a)=c:(a b),求x的值.
【误解】由等比性质得 x=(a b c):2(a b c)=1/2.
【点评】上面的解法只考虑了a b c≠0的情况,而忽略了a b c=0的情况。当a b c=0时,b c=-a,c a=-b,a b=-c,所以x=-1.故x=1/2或x=-1.所以,我们在运用等比性质解题时,不能忽略后项和为零的情况.
,