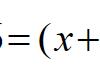思路探寻:以二次项系数是正数为例(如果二次项系数是负教,可以提一个负号变为正数),二次项分解为两个正因数的积,常数项是正数时,分解为两个同号因数的积,符号与一次项系数符号相同;如果是负数,分解为两个异号因数的积,绝对值较大的数的符号与一次项系数符号相同。
题型三、含有两个字母的二次三项式的因式分解
思路探寻:把其中任意一个字母当作“主”元,另一个当作一个数,然后写成“主"元降幂排列的二次三项式。

分解方法仍然是“拆两头,凑中间。横写加法,因式相乘。"只是记住写上字母。
题型四、“双十字相乘法”
“双十字相乘法”指用此法两次。方法一、①前三项结合分解成两个因式的积;②把这两个因式当作两个数,再用十字相乘法。因为有两个字母,所以凑中间时一定要检验每一个字母的系数是否相同。
方法二、把其中一个字母当做“主元”,然后按“主元”降幂排排列写成二次三项式,这时常数项是另外一个字母的二次三项式。先对常数项用十字相乘法分解,把分解后的两个因式当作两个数再次用“十字相乘法”分解。

题型五、转化为用“十字相乘法”分解的形式。
①分解因式ab b^2 a一b一2
=b^2 (a一1)b (a一2)
思路探寻:转化为关于b的二次三项式,再用“十字相乘法"分解。
②分解因式(X一y)(2X一2y一3)一2
=(X一y)[2(X一y)一3]一2
=2(Ⅹ一y)^2一3(X一y)一2
思路探寻:把(Ⅹ一y)作为一个整体化成关于(X一y)的二次三项式,再用“十字相乘法"进行分解。

我是数学山人行,欢迎关注!!!