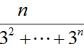鸽巢问题之最差原则
2018年8月4日星期六
“鸽巢问题”是小学数学教材中的最后一个内容。教材以3个具体示例使学生具体感知这一类问题。如图,图片来源于“电子课本网”。



人教版六年级数学下册68、69、70页
继而介绍了“抽屉原理”,如图。

人教版六年级数学下册70页
人们把由解决一类鸽巢问题中共通的思路、方法、结论,抽象概括出来的数学原理,称为“抽屉原理”,也叫“鸽巢原理”、“狄里克雷原理”、“重叠原理”。
本文基于小学数学教材展开,同时希望有所延伸。
“鸽巢原理”朴素而重要,在很多解决问题中往往能起到“山重水复疑无路,柳暗花明又一村”的神奇效果,也就是说,它能提供我们一种解决问题的崭新的、有效的出路。
良好地运用“鸽巢原理”,需要把握“鸽巢原理”运用中的“术”和“道”。“术”指方法,鸽巢原理中的“术”指运用鸽巢原理时所遵循的“最差原则”。“道”指道理,鸽巢原理的“道”在于深入理解问题的本质,构建恰当的“鸽巢”,明确“鸽巢”和“鸽子”在实际问题中的具体所指。
(重要程度★★★★★)
自本文起,共分两篇,分别讲述。
例1 把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。为什么?
本例对应的“鸽巢原理”抽象地描述为:“把n 1个元素划分至n个集合中,至少存在某个集合,包含的元素个数值大于或等于2。”
最差原则,是考虑所有可能情况中,最不利于某件事情发生的情况,也可以称为“最不利原则”。 (重要程度★★★★★)
“把4支铅笔放进3个笔筒中”,不考虑笔筒的顺序,一共有4种情况:(4,0,0)、(3,1,0)、(2,2,0)、(2,1,1),如图。

“至少有2支铅笔”的意思是:铅笔数≥2;“总有一个笔筒里至少有2支铅笔”的反面是“所有笔筒里的铅笔数都<2”。最不利原则可以理解为我们最不希望看到“总有一个笔筒里至少有2支铅笔”发生,而最希望看到“所有笔筒里的铅笔数都<2”发生。
为了便于描述,我们约定:
“总有一个笔筒里至少有2支铅笔”:事件A
情况(4,0,0):当放入第2支铅笔时,事件A发生;
情况(3,1,0):考虑“最差”,当放入第3支铅笔时,事件A发生;
情况(2,2,0):考虑“最差”,当放入第3支铅笔时,事件A发生;
情况(2,1,1):考虑“最差”,当放入第4支铅笔时,事件A发生。
综合对比,本例中“最不利情况”为(2,1,1),描述为:先给每个笔筒里放1支铅笔,此时共放3支,如果继续放第4支,则A必然发生。所以:把4支铅笔放进3个笔筒中,总有一个笔筒里至少有2支铅笔。
上面的“最不利情况”有个特点:先均分至事件A的反面,即“所有笔筒里的铅笔数都<2”,然后再加1,不管如何,结论得证。现在,您或许可以理解老师教给我们的列算式解答背后的道理了:
4÷3=1(支)……1(支)
1+1=2(支)
例2 把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?如果有8本书会怎样呢?10本书呢?
本例对应的“鸽巢原理”抽象地描述为:“把nm 1个元素划分至n个集合中,至少存在某个集合,包含的元素个数值大于或等于m 1。”
根据“最不利原则”,我们最不希望“总有一个抽屉里≥3本”发生,故而先给每个抽屉“均分”2本,共分2×3=6本。此时,当第7本书出现,则必然导致“总有一个抽屉里至少放进3本书”这一事件发生。用算式描述过程为:
7÷3=2(本)……1(本)
2+1=3(本)
后面追加的两问旨在强调,方法为“商+1”,而非“商+余数”。(重要程度★★★★)
如果有8本书时:
8÷3=2(本)……2(本)
2+1=3(本)
结论仍旧为:“不管怎么放,总有一个抽屉里至少放进3本书。”正确情况为:(3,3,2),而不是(4,2,2),因为这两种情况必然能满足“总有一个抽屉里≥3”,但不一定能满足“总有一个抽屉里≥4”。
如果有10本书时:
10÷3=3(本)……1(本)
3+1=4(本)
结论为:“不管怎么放,总有一个抽屉里至少放进4本书。”
例3 盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
本例的重点在于辨析不同的“鸽巢”。以颜色种数为“鸽巢”,加1得到的结果“3个”为正解。但“摸出5个球,肯定有2个同色的”这种错误也值得深思和警惕。
将问题修改为“要想摸出的球一定有2种颜色,至少要摸出几个球”,则上面的“摸出5个球”成为正解。此时“鸽巢”变为各种颜色球的最大个数。(重要程度★★★★)
进一步地,将例3修改如下:
“盒子里有同样大小的红球4个、蓝球6个,要想摸出的球一定有2种颜色,至少要摸出几个球?”
Max{4,6}=6(个) (应用最不利原则)
6+1=7(个)
答:至少摸出7个球,摸出的球才能一定有2种颜色。
很明显,一开始我们一直假定“摸出的是同色的球”,要么连续4个红球,要么连续6个蓝球,后者是最不利情况。
下面是一道经典的题,来源于匈牙利大数学家厄杜斯(1913~1996)给当年年仅11岁的波萨提出的问题,小波萨思考了不足半分钟便能给出正确的答案。我对原题进行了改编,并从不同的角度予以分析、阐释。
“已知1~100的自然数,问:至少取出多少个数,才能保证一定有至少2个数互质?”
大家先独立思考下……
……
……
……
……
……
……
……
……
……
……
……
……
……
……
……
……
……
……
……
……
有没有一种“无处下手”的感觉?让我们慢慢来……
公因数只有1的两个数叫做互质数。一定是互质数的情况大约有(下面讨论的“自然数”遵循通常约定:不包含0):
①1和任何自然数是互质数,如:(1,8)=1;
②两个不同的质数是互质数,如:(5,11)=1;
③两个连续的自然数是互质数,如:(5,6)=1;
④两个连续的奇数是互质数,如:(15,17)=1;
⑤两个相差4的奇数是互质数,如:(21,25)=1;
⑥一个质数和一个合数,没有倍数关系时,是互质数,如:(7,20)=1,其中:7∤20;
……
上面罗列的6种情况中:①②⑥可以进行正面说明,③④⑤需要用“反证法”证明,大抵是“假设两自然数m、n并不互质,而是存在大于1的公因数a,然后推导出矛盾,即可得证”,此处略去。需要强调的是:大多数情况下,任意两个自然数是否互质,是难以直接简单判断的。
什么叫“一定有至少2个数互质”?我们来考察这个问题的反面:所有的数两两都不互质。此时,这组数除了公因数1外,还有其他的公因数,比如:2、3、4、5、6……或为其中1个,或为其中2个、3个、任意个。
有公因数2的自然数集合为2的倍数的集合或其子集:
{2,4,6,8,10,12,14……}
有公因数3的自然数集合为3的倍数的集合或其子集:
{3,6,9,12,15,18,21……}
有公因数4、6的自然数集合为12的倍数的集合或其子集,因为[4,6]=12:
{12,24,36,48,60,72,84……}
有公因数5、9、15的自然数集合为45的倍数的集合或其子集,因为[5,9,15]=45:
{45,90,135,180,225,270,315,360……}
……
总结:所有两两都不互质的自然数集合(或无限集合,或有限集合),必为某一自然数的倍数的集合或其子集。(重要程度★★★★)
情况一:我们以不超过100的2的倍数的子集作为“鸽巢”:
{2,4,6,8,10,12,14,……,98,100}
共有50个“鸽巢”。此时,任意增加一个剩余的数,都必将与其中两个相邻的2的倍数连续,由于“连续两个自然数是互质数”,因此取出50+1=51个数,符合题意;
情况二:我们再以不超过100的3的倍数的子集作为“鸽巢”:
{3,6,9,12,15,……,96,99}
共有33个“鸽巢”。此时,任意增加一个剩余的数,都必将与其中1个3的倍数连续,由于“连续两个自然数是互质数”,因此取出33+1=34个数,符合题意;
情况三:我们再以不超过100的4的倍数的子集作为“鸽巢”:
{4,8,12,16,20,……,96,100}
共有25个“鸽巢”。此时,任意增加一个剩余的数,并不能必然产生至少2个互质数,比如增加一个6,因此该“鸽巢”构建失败;
……
可以想见:以上“情况一”中的“鸽巢”是100以内满足“两两都不互质”的规模最大的“鸽巢”。根据“最不利原则”,34<51,51是正解,即:
“从1~100的自然数中,至少取出51个数,才能保证一定有至少2个数互质。”
本例的解题过程中,除了应用“最差原则”,“构建鸽巢”更为重要。但本文的重点依然在于“最差原则”,当您阅读完下文“构建鸽巢”后,亦可回过头来对此例再度审视。
好的,再会。欲知后事如何,且听下回分解。
,