题目:在三角形ABC中,∠A:∠B:∠C=1:2:4,∠A,∠B,∠C所对的边分别为a,b,c,求证:1/a=1/b 1/c

解法一:如果一个三角形的一个内角等于另一个内角的两倍,我们称这样的三角形为“倍角三角形”。倍角三角形的性质之一:两倍角和单倍角所对边的平方差等于单倍角所对边与第三边的积。依据这个原理,我们可见本题中有两个两倍角关系,分别列出两个代数式。
1.∠B=2∠A:b ²-a ²=a·c
2.∠C=2∠B:c ²-B ²=b·a
经代数运算即可证明1/a=1/b 1/c成立。
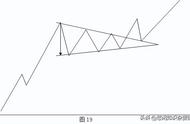
解法二:如图2,延长AC到D,使CB=CD;AB上取E点,使CB=CE。连接BD。根据辅助线及180°=7θ逐一标出各角大小于图中,得出以下关系。
△BCE≌△BCD,BE=BD=c﹣a。
△ABC∽三角形ADB,AB/AD=AC/AB=BC/BD,即c/a b=b/c=a/c-a。经代数运算即可证明等式成立。

解法三:将三角形ABC三边通过等量代换构造一个经典的“山”字标准图形()。如图3,过A点作AD平行于BC,使AD=AB,连接DB并延长交AC的延长线于E点,过E作EF平行于BC交AB延长线于F。这样就可以得出1/a=1/c 1/EF,剩下证明EF=AC=b就行了。在CE上取G点,使BG=BC,根据图中线段和角度关系,可以证明△FGE全等于三角形ABC,这样EF=AC=b,最终证明1/a=1/b 1/c。