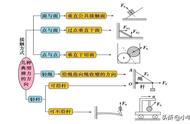
物体受弹力的方向和大小判断
弹力也是被动的接触力(即只能在两个相互接触的物体之间产生),高中学到的弹力形式主要有:
弹簧产生的弹力,物体之间挤压产生的弹力,绳子产生的弹,硬杆产生的弹力等。
这些弹力的大小、方向与物体的运动状态有联系——物体的受力情况决定了物体的运动状态;物体的运动状态反映了物体的受力情况。这是判断弹力有无以及产生的大小和方向的重要依据。
基本方法是,根据牛顿第二定律F=ma以及牛顿第三定律,结合物体运动的加速度,判断弹力的有无及大小和方向。
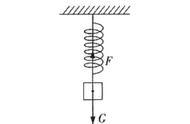
例1、如图,被托住的A重100牛顿,用细绳通过定滑轮连接的B物重60牛顿,定滑轮用弹簧秤固定在天花板上,现在系统保持静止,滑轮质量不计,则弹簧秤的读数为多少?若将托住A的支持物撤去,弹簧秤的读数又为多少?(g=10米/秒²)

例1
解:从物体的状态看
(1)开始A物体被托住时,所有物体都处于静止状态
由力的平衡方程可知,
对B物的拉力:T₁=GB=60牛顿
由牛顿第三定律可知,对A物的拉力T₂= T₁=120牛顿
滑轮处于一个平衡状态,
∴ 定滑轮受的弹簧的弹力T=2T₁=120牛顿
此时弹簧秤的读数应为120牛顿
(2)撤去A物体的支持物,系统发生运动,
A向下运动,B向上运动,加速度大小相等,
将A、B两物体和绳子看作一个整体(整体法),
应用牛顿第二定律,
(GA-GB)=(mA mB)a
∴ a=(GA-GB)/(mA mB)=2.5米/秒²
对于B(隔离法):
应用牛顿第二定律,
T₁-GB= mB a
∴T₁=75牛顿
对于定滑轮(隔离法)处于静止状态,
有力的平衡方程可知,
则弹簧的弹力 T=2T₁=150牛顿
此时弹簧秤的读数应为150牛顿
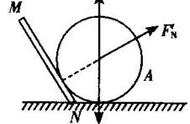
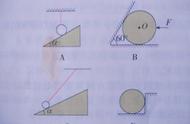
例2、一个光滑的圆锥体固定在水平的桌面上,其轴线沿竖直方向,母线与轴线之间的夹角θ=30º,一条长度为L的绳(质量不计),一端的位置固定在圆锥体的顶点O处,另一端拴着一个质量为m的小物体(物体可看作质点),物体以速率V绕圆锥体的轴线做水平匀速圆周运动(物体和绳在图中都没画出)。
(1)当V= √(gL/6)时,求绳对物体的拉力
[ "√ "符号的意思是:(gL/6)开平方,以下表示同此理]
(2)当V= √(3gL/2)时,求绳对物体的拉力

例2
解:物体在水平面上做匀速圆周运动,
可能有两种情况:
一种是物体与锥体表面接触,
另一种是物体与锥体表面不接触。
这取决于物体做圆周运动的速度大小,
设物体与锥面接触,
将物体所受的力,分解在水平和竖直两个方向上,
分别用牛顿第二定律,则有:
水平方向: Tsinθ-Ncosθ=mv²/Lsinθ ①
竖直方向: Tcosθ Nsinθ=mg ②
两式联立得:N=mgsinθ-mv²cosθ/Lsinθ
若 N=0,θ=30º时
有 V= √((√3)gL/6)
所以,物体以速率V绕圆锥体的轴线做水平匀速运动的情况,有三种:
(a)当V< √((√3)gL/6)时,
物体与锥体表面接触,且有支持力N,
(b)当V= √((√3)gL/6)时,
物体与锥体表面接触,支持力N=0
(c)当V> √((√3)gL/6)时,
物体与锥体表面不接触,无支持力N,并且物体离开圆锥体表面
所以:
(1)当V= √(gL/6)<√((√3)gL/6)时,
物体与锥体表面接触,且有支持力N,
由①和②联立得:
T=mv²/L mg cosθ
=(1 3 √3)mg/6

例2第(1)种情况分析图
(2) 当V= √(3gL/2)>√((√3)gL/6)时,
∴ 物体不与锥面接触,只受重力和绳子的拉力做圆周运动,
则有:
Tsinθ=mV²/Lsinθ ①
Tcosθ=mg ②
消去θ得(此时θ未知,已经大于30°),
(消去θ的时候要用到公式:sin²θ cos²θ=1)
T²-(mV²/L)T-m²g²=0
代入V的数据的,
2T²-3mgT-2m²g²=0
∴ T=2mg

例2第(2)种情况分析图
此例可看出T的大小与物体的运动状态有关(实际上是T的大小和方向决定了物体的运动状态)。
不但如此,物体与斜面之间作用力N的大小也与物体做匀速圆周运动的速度有关:
N= mgsinθ-mv²cosθ/Lsinθ
当V=0时,N最大为mgsinθ,
随着V增大,N则减小,
当V为√((√3)gL/6)时,N=0
例2分析过程中,选择了物体与锥体表面接触做圆周运,但此时N为0的状态,这个状态叫做临界状态,此时得出临界速度V= √((√3)gL/6),这是分析此类问题的一个关键,在前一讲关于静摩擦力大小和方向的判断中,两道例题也都用到了临界状态的分析方法,这是高中物理学习中的一个重要的物理思想,熟练掌握受益无穷。
,