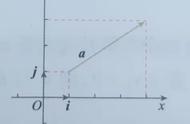头条邀请我回答下面的问题:

为什么目前所应用的坐标系先写x后写y?这算一个问题吗?我的回答是,这种问法,非数学本质:
①笛卡尔坐标系只是一种一一对应(一一映射)的特殊情况—函数,如果颠倒过来也是可以的,就是一个函数的反函数(前提是这个函数得有反函数)。反函数的核心是原函数反解表达式(用y表示x)唯一,再交换x,y,但交换非必须的,只是为了符合用x做自变量的习惯。
②不一定非得是直角坐标系,斜坐标系也是有的,但无论如何,在Ω²中,得有一对有序的实数对应一个点。
③笛卡尔坐标系可以认为是一个向量空间,取两个正交的向量即可。这事,推广到n维空间亦可,在那儿,一般的坐标写成(x1,x2,……,xn),你还要问x1为什么要写在第一个吗?
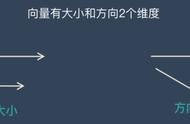
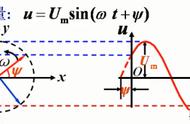
④实际上,有时为了研究方便,图形和有序实数的对应,未必非写成(x,y)的样子,比如写成x yi(复数),或写出起始点AB上面加上→(向量),这也解释了为嘛高考主要考向量,而基本不考复数的原因。若回到1980年代,你看那时考的是啥?
⑤要说历史原因,符号学的变迁多了去了,任何一个数学符号的固化都有一个历史过程,有的到现在也不统一,比如排列组合的记号,国外的数学书上现在还记为C(m,n),这与现行的高中课本有很大的判别,又如过去一度国内把正切记为tg,后来据说为了与国际接轨,记成了tan,习惯就好,也没有什么特别的.只是看过去的书,要了解这个历史,就像看古书中的繁体字,认识即可.
⑥如果是你自己独创的一套数学理论,里面的记号随你自己来定喽!比如那个据称解决了ABC猜想的日本的望月新一,他的论文里就是一些天书的记号呢!


怪不得世界人民看不动!据说连陶哲轩也看着吃力呢.
最后说一点,有时我们也用(u,v)来写一个点,你说为什么先写u而不是先写v呢?
,