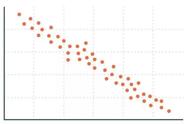
本篇讨论一个有趣的话题,我们将概率论和线性代数结合起来,看看协方差和相关系数在线性代数中如何解释。
本篇较为硬核。原因是一般对协方差和相关系数,特别是相关系数,的讨论,都给人感觉云里雾里。我估计原因可能是身在此山中。所以我们需要跳出概率论看着两个概念,由于相关系数的推导过程涉及了线性代数中的最小二乘,所以非常自然地,我们可以从线性代数入手,考察协方差和相关系数的意义。毕竟,线性代数中的概念有非常直观的几何意义。曲线救国,从线性代数入手,将概率论数形结合。
柯西——施瓦茨不等式首先回顾一下线性代数中的内积和夹角。
内积空间V中两个向量x,y比满足

于是可以用柯西——施瓦茨不等式定义夹角

对比观察相关系数的定义

于是我们好像发现了