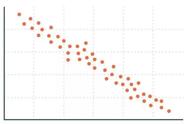
正相关性指的是两个变量之间的变化趋势是一致的现象。换句话说,当一个变量的增加伴随着另一个变量的增加,或者一个变量的减少伴随着另一个变量的减少时,这两个变量就呈现出正相关性。在统计学中,正相关性通常使用皮尔逊相关系数来进行衡量,取值范围在-1到1之间,值越接近1则代表正相关性越强。举个例子,研究人员发现,随着一个国家的人均收入提高,其人均寿命也会相应增加,这就是正相关性的一个实际案例。在这个案例中,两个变量——人均收入和人均寿命呈现出了正相关的关系。
数学表示方面,正相关性通常使用皮尔逊相关系数来进行衡量。皮尔逊相关系数的计算方法是通过协方差除以两个变量的标准差的乘积,这个数值的正负号表示了变量之间的关系是正相关还是负相关,而数值的大小则表示了相关性的强弱。在实际案例分析中,可以以市场营销中产品销量和广告投入之间的关系为例。通过对历史数据的统计分析,可以得出产品销量和广告投入呈现出一定程度的正相关性。这意味着随着广告投入的增加,产品销量也相应增加,反之亦然。这种正相关性的存在为企业的营销决策提供了重要的参考依据。
负相关性的概念解释
负相关性指的是两个变量之间的变化趋势是相反的现象。也就是说,当一个变量的增加伴随着另一个变量的减少,或者一个变量的减少伴随着另一个变量的增加时,这两个变量就呈现出负相关性。在统计学中,负相关性同样使用皮尔逊相关系数来进行衡量,取值范围在-1到1之间,当相关系数的值接近-1时则代表负相关性越强。举个例子,研究人员发现,随着气温的升高,冰淇淋的销量会下降,这就是负相关性的一个实际案例。在这个案例中,气温和冰淇淋销量呈现出了负相关的关系。
数学表示方面,负相关性同样使用皮尔逊相关系数来衡量。皮尔逊相关系数的计算方法同样是通过协方差除以两个变量的标准差的乘积,负号表示了变量之间的关系是负相关,而数值的大小则表示了相关性的强弱。在实际案例分析中,可以以天气状况和雨伞销量之间的关系为例。通过对历史数据的统计分析,可以得出天气状况和雨伞销量呈现出一定程度的负相关性。这意味着随着天气变好,雨伞销量会相应下降,反之亦然。这种负相关性的存在为零售商的库存管理和市场预测提供了重要的参考依据。
负相关性的数学表示与实际案例分析
在统计学中,负相关性是指两个变量之间的变化趋势是相反的现象。当一个变量的增加伴随着另一个变量的减少,或者一个变量的减少伴随着另一个变量的增加时,这两个变量就呈现出负相关性。负相关性的存在通常会导致一个变量的增加与另一个变量的减少,或者一个变量的减少与另一个变量的增加之间形成某种规律上的关联。在统计学中,我们通常使用皮尔逊相关系数来衡量负相关性,其取值范围在-1到1之间,当相关系数的值接近-1时,则代表负相关性越强。
为了更好地理解负相关性,让我们以天气状况和雨伞销量之间的关系为例进行实际案例分析。通过对历史数据的统计分析,我们发现天气状况和雨伞销量呈现出一定程度的负相关性。具体而言,天气变好的情况下,雨伞的销量通常会出现下降的趋势;而在天气变差或下雨的情况下,雨伞的销量则往往会有所增加。这种负相关性的存在为零售商的库存管理和市场预测提供了重要的参考依据。通过对天气状况和雨伞销量之间的负相关性有所了解,零售商可以更准确地控制雨伞的库存量,以及制定更有针对性的促销计划和市场营销策略,从而更好地满足顾客的需求,提高销售效益。
通过负相关性的数学表示和实际案例分析,我们可以更好地理解和应用这一统计学概念。不论是在商业决策、市场营销还是科学研究领域,对于负相关性的深入理解和运用都将为我们带来更准确的数据分析和预测能力,进而提高工作效率和决策水平。因此,通过深入研究正相关性和负相关性的比较,我们可以更好地把握变量之间的关联规律,为未来的研究和实践工作提供更有力的支持和指导。
在未来,我们可以进一步探讨更多领域内的相关性现象,丰富我们对相关性规律的认识,并将相关性的概念和方法应用于更广泛的实际问题中,进一步提升我们的数据分析和决策能力。因此,通过对正相关性和负相关性的深入了解和应用,我们将不断推动统计学理论的发展和实践应用,为社会各个领域的进步和发展贡献我们的力量。
正相关性和负相关性是统计学中两个重要的概念,它们分别描述了两个变量之间的变化趋势是一致的现象和相反的现象。首先,正相关性表示当一个变量的增加伴随着另一个变量的增加,或者一个变量的减少伴随着另一个变量的减少时,这两个变量就呈现出正相关性。正相关性通常用皮尔逊相关系数来衡量,其数值范围在-1到1之间,数值越接近1则代表正相关性越强。举例来说,国家的人均收入与人均寿命呈现出了正相关的关系,这说明收入增加会导致寿命延长。
而负相关性则表示当一个变量的增加伴随着另一个变量的减少,或者一个变量的减少伴随着另一个变量的增加时,这两个变量就呈现出负相关性。在统计学中,同样使用皮尔逊相关系数来衡量负相关性,其取值范围也在-1到1之间,当相关系数的值接近-1时,则代表负相关性越强。例如,天气变好时,雨伞销量通常会下降,天气变差或下雨时雨伞销量则会增加。
总体而言,正相关性和负相关性都是衡量变量之间关联程度的重要指标,它们的应用涵盖了各个领域,包括科学研究、商业决策和市场营销等。通过对它们的深入理解和具体应用,我们能够更准确地把握变量之间的关联规律,为决策和预测提供更可靠的参考依据。因此,在未来的研究和实践中,对正相关性和负相关性的进一步探讨和应用将会为各个领域的发展贡献力量,推动统计学理论的不断完善和实践应用的深入发展。
正相关性和负相关性作为统计学中的两个重要概念,对于描述变量之间关联程度具有重要意义。正相关性指的是两个变量之间的变化趋势是一致的现象,而负相关性则表示变量之间的变化趋势是相反的现象。下面我们将通过正相关性和负相关性的概念解释、数学表示以及实际案例分析,来深入探讨这两个概念,并进行比较分析。
首先,正相关性描述了两个变量之间变化趋势一致的情况。大多数情况下,人们使用皮尔逊相关系数来衡量正相关性,其取值范围在-1到1之间,数值越接近1则代表正相关性越强。举例而言,在国家经济发展领域,人均收入的增加往往伴随着人均寿命的延长,这就是正相关性的一个实际案例。数学表示方面,正相关性通过皮尔逊相关系数进行衡量,而在实际案例分析中,可以以产品销量和广告投入之间的关系来进行具体分析,这为企业的营销决策提供了实质性的参考依据。
与正相关性相对应的是负相关性,它描述了两个变量之间的变化趋势是相反的现象。同样使用皮尔逊相关系数来衡量负相关性,其取值范围在-1到1之间,相关系数的值接近-1时则代表负相关性越强。举例而言,随着气温的升高,冰淇淋的销量通常会下降,这就是负相关性的一个实际案例。在实际案例分析中,天气状况和雨伞销量之间的关系则展现了一定程度的负相关性,这为零售商的库存管理和市场预测提供了重要的参考依据。
正相关性和负相关性分别描述了两个变量之间变化趋势的一致性和相反性,它们在实际应用中具有广泛的价值。进一步地,对正相关性和负相关性的深入研究与应用,将为我们提供更准确的数据分析和预测能力,进而提高工作效率和决策水平。因此,通过对正相关性和负相关性的比较分析,我们可以更好地把握变量之间的关联规律,为未来的研究和实践工作提供更有力的支持和指导。
正相关性和负相关性作为统计学中的两大概念,其对于对两个变量之间的变化趋势的描述具有重要的现实意义。正相关性指的是两个变量之间的变化趋势呈现一致的现象,而负相关性则表示变量之间的变化趋势是相反的现象。通过对正相关性和负相关性的概念解释、数学表示以及实际案例分析,我们能够更加深入地理解它们,并在实际应用中加以运用和分析。期待未来,我们可以进一步探讨更多领域内的相关性现象,丰富我们对相关性规律的认识,并将相关性的概念和方法应用于更广泛的实际问题中,进一步提升我们的数据分析和决策能力。
通过对正相关性和负相关性的深入了解和应用,我们将不断推动统计学理论的发展和实践应用,为社会各个领域的进步和发展贡献我们的力量。在未来的研究和实践中,对正相关性和负相关性的进一步探讨和应用将会为各个领域的发展贡献力量,推动统计学理论的不断完善和实践应用的深入发展。期待着正相关性和负相关性的研究能够为我们的工作和生活带来更多可能性和机遇。
,