一、引言
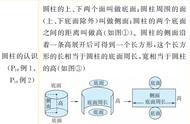
在数学空间中,棱柱、棱锥和棱台是常见的几何体。对于这几种几何体,计算它们的表面积和体积是数学学习中的重要内容。本文将详细介绍如何计算棱柱、棱锥和棱台的表面积和体积,帮助同学们更好地掌握这一知识点。

二、棱柱的表面积和体积
- 棱柱的表面积
棱柱的表面积等于其所有面的面积之和。具体计算公式如下:
表面积 = 2 × 底面积 侧面积
其中,底面积为棱柱底面多边形的面积,侧面积为棱柱所有侧面的面积之和。对于直棱柱,侧面积等于底面周长与高的乘积。
- 棱柱的体积
棱柱的体积等于其底面积与高的乘积。具体计算公式如下:
体积 = 底面积 × 高
三、棱锥的表面积和体积
- 棱锥的表面积
棱锥的表面积等于其所有面的面积之和。具体计算公式如下:
表面积 = 底面积 侧面积
其中,底面积为棱锥底面多边形的面积,侧面积为棱锥所有侧面的面积之和。对于正棱锥,侧面积等于底面周长与斜高(侧面上的高)乘积的一半。
- 棱锥的体积
棱锥的体积等于其底面积与高的乘积的三分之一。具体计算公式如下:
体积 = (1/3) × 底面积 × 高
四、棱台的表面积和体积
- 棱台的表面积
棱台的表面积等于其所有面的面积之和。具体计算公式如下:
表面积 = 上底面积 下底面积 侧面积
其中,上底面积和下底面积分别为棱台上、下底面多边形的面积,侧面积为棱台所有侧面的面积之和。对于正棱台,侧面积等于上、下底面周长之和与斜高(侧面上的高)乘积的一半。
- 棱台的体积
棱台的体积可以使用以下公式计算:
体积 = (1/3) × (上底面积 下底面积 √(上底面积 × 下底面积)) × 高
这个公式是通过将棱台划分为三个三棱锥,然后分别计算它们的体积并相加而得到的。这种方法可以简化计算过程,并且适用于所有类型的棱台。
五、典型例题分析
- 例1:一个正四棱柱的底面边长为4cm,高为6cm,求其表面积和体积。
解:正四棱柱的底面积为4² = 16cm²,底面周长为4×4 = 16cm。因此,侧面积为16×6 = 96cm²。所以,表面积为2×16 96 = 128cm²。体积为16×6 = 96cm³。 - 例2:一个正三棱锥的底面边长为6cm,高为4cm,求其表面积和体积。
解:正三棱锥的底面积为(√3/4) × 6² = 9√3cm²,底面周长为3×6 = 18cm。斜高可以通过勾股定理求得为√(4² (6/2)²) = √25 = 5cm。因此,侧面积为(1/2) × 18 × 5 = 45cm²。所以,表面积为9√3 45cm²。体积为(1/3) × 9√3 × 4 = 12√3cm³。 - 例3:一个正四棱台的上底面边长为2cm,下底面边长为6cm,高为4cm,求其表面积和体积。
解:正四棱台的上底面积为2² = 4cm²,下底面积为6² = 36cm²。上底面周长为4×2 = 8cm,下底面周长为4×6 = 24cm。斜高可以通过勾股定理求得为√(4² ((6 - 2)/2)²) = √17cm。因此,侧面积为(1/2) × (8 24) × √17 = 16√17cm²。所以,表面积为4 36 16√17 = 40 16√17cm²。体积为(1/3) × (4 36 √(4×36)) × 4 = (1/3) × (40 24) × 4 = (256/3)cm³。
六、总结与展望
通过本文的学习,同学们应该已经掌握了如何计算棱柱、棱锥和棱台的表面积和体积的方法。这些知识点在高中数学中占有重要地位,希望同学们能够认真学习和掌握。同时,也期待教育工作者和研究者们能够不断完善和拓展这一领域的教学内容和方法,为学生提供更加优质的教育资源和指导。