学习完现金流量和资金的时间价值的一些概念后,我们来学习利息的计算方式以及等值计算,利息的计算方法(复利计算比较易考)理解做题后就可以掌握,重点学习的就是等值计算,这个不仅仅是易考点,还是难点。难就难在公式的记忆以及推导上。
一、利息的计算方法

补充:1)单利:I=P*i (I — 利息额,P— 本金,i — 利率)
表格中单利的那个公式中F表示n期末单利本利和。(1 n*i)表示单利终值系数。
2)复利
①同一笔借款,在利率和计息数均相同的情况下,用复利计算出的利息金额比用单利计算出的利息金额大。
②本金越大,利率越高,计息期数越多时,两者差距就越大。工程经济中,一般采用复利计算。
二、等值计算(★★★★★)
(一)影响资金等值的因素
等值(也称为等效值):不同时期、不同数额但其“价值等效”的资金。
影响资金等值的因素有三个:资金多少、资金发生时间、利率(折现率)大小。其中利率是一个关键因素。
(二)等值计算方法

注:该部分涉及到三个值,这个是要重点区别的哦:
P — 现值(某一特定时间序列起点时的价值);
F — 终值(某一特定时间序列终点时的价值);
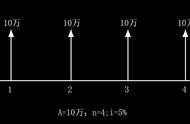
A — 年值【发生在(或折算为)某一特定时间序列各计息期末(不包括0期)的等额支付系列价值】
注:现值,present worth;终值,final value;年值,Annual value
根据英文单词记忆这三个词会更容易点,毕竟这三个字母是学习这章的重中之重。
1、一次支付(整付)情形
1)终值计算——已知P求F
公式:F=P(1 i)n=P(F/P,i,n)
(1 i)n —— 成为一次支付终值系数,用(F/P,i,n)表示
注:(F/P,i,n),斜线左侧表示所求的未知数,即F值; 斜线右侧表示已知数,即P,i,n。
2)现值计算:P=F(1 i)-n=F(P/F,i,n)
(1 i)-n —— 一次支付现值系数,用(P/F,i,n)表示,也称为折现系数或贴现系数。

2、等额支付系列情形
1)终值计算