净现值是一项投资所产生的未来现金流的折现值与项目投资成本之间的差值。净现值指标是反映项目投资获利能力的指标。
决策标准:
- 净现值≥0 方案可行;
- 净现值<0 方案不可行;
- 净现值均>0 净现值最大的方案为最优方案。
下面看看如何进行净现值的计算。
某公司进行一项投资,假设第一年年末投资100000元,在投资后的4年中每年可以获得收益分别为:20000元,28000元,42000元,38000元,假定年折现率为5%,求该投资的净现值。
按照净现值的定义,我们需求出现金流入的现值和现金流出的现值,然后二者相减即可。
现金流入现值为:
20000/1.05^2 28000/1.05^3 42000/1.05^4 38000/1.05^5=106655.5
现金流出现值为:100000/1.05=95238.1
净现值为:106655.5-95238.1=11417.45
下面我们用财务函数NPV求其净现值。NPV功能是基于一系列现金流和固定的各期利率,计算一组定期现金流的净现值。
语法公式:NPV(rate,value1,value2……)
rate为各期折现率
value1,value2……代表现金流入和流出的参数值,流出为负值,流入为正值,而且各期间长度相等,并且现金流入或流出发生在期末。
我们在EXCEl进行录入函数公式进行其净现值计算:
=NPV(5%,-100000,20000,28000,42000,38000)
计算结果为11417.45

再看一例:
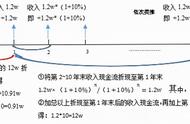
某公司有一投资方案,假设第一年初投资100000,投资当年可或收益10000,以后四年中的每年均可获收益30000,假定年折现率5%,那么该投资的净现值为多少?
在Excel中计算录入公式:
=NPV(5%,10000,30000,30000,30000,30000)-100000

如果上面2项投资方案需要进行取舍的话,因为第一项投资方案净现值大于第二项投资方案净现值,所以我们应该选择第一种投资方案。
净现值函数NPV在使用时需要注意以下几点:
1、各现金流间隔期必须相等
2、要求现金流发生在各期期末,如果发生在期初,需将第二期期初的现金流作为第一期期末的现金流,后面依次类推。
3、要区别于现值函数PV,PV计算的是各期相等现金流的现值,属于年金现值函数,而求一组不等额现金流现值时,应使用NPV函数计算。
,