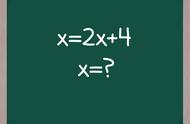试卷副标题
考试范围:xxx;考试时间:100分钟;命题人:xxx
学校:___________姓名:___________班级:___________考号:___________
【1.题】已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是( )
A.2
B.4
C.5
D.7
【2.题】下列命题:
①两条直线被第三条直线所截,同位角相等;
②两点之间,线段最短;
③相等的角是对顶角;
④直角三角形的两个锐角互余;
⑤同角或等角的补角相等.
其中真命题的个数是( )
A.2个
B.3个
C.4个
D.5个
【3.题】如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于( )
A.35° B.45° C.55° D.65°
【4.题】如图所示,AB∥CD,AF与CD交于点E,BE⊥AF,∠B=65°,则∠DEF的度数是( )
A.15°
B.25°
C.30°
D.35°
【5.题】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )
A.∠AOC=40°
B.∠COE=130°
C.∠EOD=40°
D.∠BOE=90°
【6.题】下列图形中,∠1与∠2是同位角的是( ).
A.
B.
C.
D.
【7.题】下列命题:①两条直线相交,一角的两邻补角相等,则这两条直线垂直;②两条直线相交,一角与其邻补角相等,则这两条直线垂直;③内错角相等,则它们的角平分线互相垂直;④同旁内角互补,则它们的角平分线互相垂直。其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
【8.题】如图,点
的坐标为
,点
在直线
上运动,当线段
最短时,点
的坐标为( )
A.
B.
C.
D.
【9.题】如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是 ______.
【10.题】如图,P为直线l外一点,A、B、C在l上,且PB⊥l,下列说法中,正确的个数是( ) ①PA、PB、PC三条线段中,PB最短 ②线段PB的长叫做点P到直线l的距离 ③线段AB是点A到PB的距离 ④线段AC的长是点A到PC的距离
A. 1个 B. 2个 C. 3个 D. 4个
【11.题】体育课上,老师测量跳远成绩的依据是( )
A.平行线间的距离相等
B.两点之间,线段最短
C.垂线段最短
D.两点确定一条直线
【12.题】以下说法正确的是( )
A.有公共顶点,并且相等的两个角是对顶角
B.两条直线相交,任意两个角都是对顶角
C.两角的两边互为反向延长线的两个角是对顶角
D.两角的两边分别在同一直线上,这两个角互为对顶角
【13.题】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C; ②∠AEF=∠AFE; ③∠EBC=∠C;④AG⊥EF.正确结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【14.题】如图,∠1和∠2是同位角的图形有 ( )
A.1个
B.2个
C.3个
D.4个
【15.题】下列图中∠1与∠2是同位角的是( )
A.
B.
C.
D.
【16.题】下列命题中是真命题的是( )
A.<span style="color: rgb(169, 68, 66); font-size: 12px; line-height: 17.1429px; background-color: rgb(245, 245, 245);">经过直线外一点,有且只有一条直线与已知直线垂直</span>
B.平分弦的直径垂直于弦。
C.对角线互相平分且垂直的四边形是菱形 。
D.反比例函数
,当k<0时,y随x的增大而增大。
【17.题】若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为( )
A.10cm
B.4cm
C.10cm或4cm
D.至少4cm
【18.题】如图,下列说法错误的是( )
A.∠A与∠EDC是同位角
B.∠A与∠ABF是内错角
C.∠A与∠ADC是同旁内角
D.∠A与∠C是同旁内角
【19.题】如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
A.40°
B.45°
C.50°
D.55°
【20.题】下列说法不正确的个数有( )
①. 两条直线被第三条直线所截,同位角相等
②. 对顶角一定相等,邻补角的和一定为1800;
③.平面直角坐标系把平面上的点分为四部分;
④. 体育老师测定同学的跳远成绩的依据是垂线段最短。
⑤.在同一平面内,三条直线a,b,c若满足a⊥b,b⊥c,则a⊥c.
A.1个
B.2个
C.3个
D.4个
【21.题】如图,直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p,q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”是(5,3)的点的个数是( )
A.2
B.3
C.4
D.5
【22.题】如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )
A.10
B.8
C.6
D.5
【23.题】下列命题中,真命题是( ).
① 相等的角是对顶角;② 同旁内角互补;③ 在同一平面内,若a//b,b//c,则a//c;④ 末位是零的整数能被5整除.
A.①②
B.③④
C.①③
D.②④
【24.题】如图,直线AB、CD相交于点OF⊥CD,∠AOF与∠BOD的度数之比为3:2,求∠AOC的度数.
【25.题】如图,直线AB、CD相交于点O,OE⊥AB,且∠DOE=5∠COE,求∠AOD的度数.
【26.题】如图,直线AB、CD、EF都相交于O,AB⊥CD,∠EOD=128°19′,求∠BOF和∠AOF的度数.
【27.题】如图,要测量 A点到河岸 BC的距离,在 B点测得 A点在 B点的北偏东30°方向上,在 C点测得 A点在 C点的北偏西45°方向上,又测得 BC=150 m.求 A点到河岸 BC的距离.(结果保留整数)(参考数据:
≈1.41,
≈1.73)
【28.题】如图,B村位于一条河的一岸,现在要将河里的水通过修建水渠引到村里进行使用,问:这条水渠该如何修,才能使到A村的距离最短,请画出图形,并说明理由?(画图可借助三角板,量角器等工具)
【29.题】如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB,OF平分∠DOB,求∠EOF的度数.
【30.题】如图,直线AB与CD相交于点O,OE⊥CD. (1)若∠BOD=28°,求∠AOE的度数. (2)若OF平分∠AOC,小明经探究发现:当∠BOD为锐角时,∠EOF的度数始终都是∠BOC度数的一半,请你判断他的发现是否正确,并说明理由.
【31.题】如图,已知AB⊥BC,BC⊥CD,BE∥CF,∠ABE=50°,求∠FCD的度数.
【32.题】直线 AB、 CD交于 O, OE⊥ CD, OF平分∠ BOC,∠ AOC=30°。求∠ EOF的度数。[来源
【33.题】如图,在4×9的方格图中, □ABCD的顶点均在格点上,按下列要求作图: (1)在 CD边上找一格点 E,使得 AE平分∠ DAB. (2)在 CD边上找一格点 F,使得 BF⊥ AE.
【34.题】陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图) 小淇同学作法如下: (1)在直线l上任意取一点C,连接AC; (2)作AC的中点O; (3)以O为圆心,OA长为半径画弧交直线l于点B,如图所示; (4)作直线AB. 则直线AB就是所要作图形. 你认为小淇的作法正确吗?如果不正确,请画出一个反例;如果正确,请给出证明.
【35.题】如图,O是直线AB上的一点,OC⊥OD,垂足为O. (1)若∠BOD=32°,求∠AOC的度数; (2)若∠AOC:∠BOD=2:1,直接写出∠BOD的度数.
【36.题】已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.其中为真命题的是____.(填写所有真命题的序号)
【37.题】如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是_____________________________________________.
【38.题】如图,已知直线AB、CD、EF相交于点O,AB⊥CD,∠DOE=127°,则∠COE= °,∠AOF= °.
【39.题】把命题“垂直于同一条直线的两直线平行”,改写成“如果…,那么…”的形式: .
【40.题】把命题“对顶角相等”改写成“如果…那么…”的形式: .
【41.题】如图:AB、CD相交于点O,OB平分∠DOE,若∠DOE=64°,则∠AOC的度数是 .
【42.题】一个角的补角与它的余角的度数比是3:1,则这个角是 度.
【43.题】如图,直线 AB 、 CD相交于点 O,
,垂足为O,如果
,则
_______.
【44.题】如图,AB⊥m,AC⊥n,垂足分别为B、A,则A点到直线m的距离是线段_____的长.
【45.题】如图,在△ ABC中 ,∠A=90 0,BD平分∠ABC,AD=2,点E是BC边上的一个动点,则线段DE的最小值为__________。
【46.题】小丽从家到河边提水,为了节省时间,她选择了家与河岸垂直的路线,理由是______.
【47.题】如图,点
是直线
上一点,
,那么
的度数是 ________.
【48.题】如图,直线
与
相交于
,
与
、
与
分别相交成直角.图中与
互补的角是________.
【49.题】小明想度量图中点
到三角形
的边
的距离,在老师的指导下小明完成了画图,那么____就是点
到直线
的距离.
【50.题】如图
,直线
与直线
、
分别交于点
、
,
与
互补. (1)试判断直线
与直线
的位置关系,并说明理由; (2)如图
,
与
的角平分线交于点
,
与
交于点
,点
是
上一点,且
,求证:
; (3)如图
,在(2)的条件下,连接
,
是
上一点使
,作
平分
,问
的大小是否发生变化?若不变,请求出求值;若变化,说明理由.
试题答案解析
【1.题】 【答案】A. 【解析】 试题分析:如图,根据垂线段最短可知:PC<3,∴CP的长可能是2,故选A.
考点:垂线段最短.
【2.题】
【答案】B
【解析】
试题分析:利用平行线的性质、互余的定义、互补的定义分别判断后即可确定正确的选项.
①两条平行线被第三条直线所截,同位角相等,错误,为假命题;②两点之间,线段最短,正确,为真命题;③相等的角是对顶角,错误,为假命题;④直角三角形的两个锐角互余,正确,为真命题;⑤同角或等角的补角相等,正确,为真命题.
考点:命题与定理
【3.题】 【答案】C 【解析】 试题分析:由已知条件和观察图形,利用对顶角相等、角平分线的性质和垂直的定义,再结合平角为180度,就可求出角的度数. 解:∵∠B0C=∠AOD=70°, 又∵OE平分∠BOC, ∴∠BOE=
∠BOC=35°. ∵OF⊥OE, ∴∠EOF=90°. ∴∠AOF=180°﹣∠EOF﹣∠BOE=55°.故选C. 点评:本题利用垂直的定义,对顶角和角平分线的性质计算,要注意领会由垂直得直角这一要点.
【4.题】
【答案】B.
【解析】
试题解析:∵AB∥CD,∠B=65°,
∴∠BED=65°,
∵BE⊥AF,
∴∠DEF=180°-65°-90°=25°.
故选B.
考点:平行线的性质.
【5.题】
【答案】C
【解析】
试题分析:首先由垂线的定义可知∠EOB=90°,然后由余角的定义可求得∠EOD,然后由邻补角的性质可求得∠EOC,由对顶角的性质可求得∠AOC.
解:由对顶角相等可知∠AOC=∠BOD=40°,故A正确,所以与要求不符;
∵OE⊥AB,
∴∠EOB=90°,故D正确,与要求不符;
∵∠EOB=90°,∠BOD=40°,
∴∠EOD=50°.故C错误,与要求相符.
∴∠EOC=180°﹣∠EOD=180°﹣50°=130°.故B正确,与要求不符.
故选:C.
【6.题】
【答案】A.
【解析】
试题分析:同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.根据同位角的定义,可知A是同位角.
故选:A.
考点:同位角、内错角、同旁内角.
【7.题】
【答案】C
【解析】试题分析:对每个命题仔细分析,判断其对错.
解:①、两条直线相交,同角的补角一定相等,这两条直线不一定垂直,错误;
②、两条直线相交,一角与其邻补角互补且相等,则这两条直线垂直;正确.
③、内错角相等,则它们的角平分线互相平行,错误.
④、同旁内角互补,则它们的角平分线互相垂直,正确;
故选C.
【点评】本题主要考查角平分线的定义、邻补角的性质和垂线等知识点,不是很难,但是要细心分析.
【8.题】 【答案】B 【解析】分析:点到直线的距离垂线段最短,过点A作直线y=-x的垂线,交点即为所求点B,再求出点B的坐标。 解:过A点作垂直于直线y=-x的垂线AB,如图所示
∵点B在直线y=-x上运动,∴∠AOB=45°,∴△AOB为等腰直角三角形,过B作BC垂直x轴垂足为C,则点C为OA的中点,则OC=BC=
.作图可知B在x轴下方,y轴的右方.∴横坐标为正,纵坐标为负。所以当线段AB最短时,点B的坐标为(
,-
)。故选B.
【9.题】
【答案】∠1 ∠2=90°
【解析】根据平角的定义可得∠1 ∠AOC ∠2=180°,再由AB⊥CD可得∠AOC=90°,所以∠1 ∠2=90°.
【10.题】
【答案】B
【解析】①根据垂线段最短,PA、PB、PC三条线段中,PB最短是正确的;
②根据点到直线的距离可得:线段PB的长叫做点P到直线l的距离是正确的;
③根据点到直线的距离可得:正确的说法是线段AB的长度是点A到PB的距离是错误的;
∵PC不垂直AC,∴线段AC的长不是点A到PC的距离,故是错误的;
所以共有2个正确的;
故选B。
【11.题】
【答案】C
【解析】试题分析:根据跳远的实际,只要量出起跳点所在的直线和落地点的距离即可,因此是根据点到直线的距离为依据,即为垂线段最短.
故选:C.
【12.题】
【答案】A
【解析】试题解析:A、有公共顶点,并且相等的两个角是对顶角,不符合对顶角的定义,错误;
B、两角的两边互为反向延长线的两个角是对顶角,且有公共顶点的两个角是对顶角,任意两个角都是对顶角的说法错误;
C、两角的两边互为反向延长线的两个角是对顶角,符合对顶角的定义,正确;
D、两角的两边分别在同一直线上,这两个角是对顶角或者邻补角,错误.
故选C.
【13.题】
【答案】C
【解析】试题解析:∵∠BAC=90°,AD⊥BC,
∴∠C ∠ABC=90°,
∠BAD ∠ABC=90°,
∴∠BAD=∠C,故①正确;
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠ABE ∠AEF=90°,
∠CBE ∠BFD=90°,
∴∠AEF=∠BFD,
又∵∠AFE=∠BFD(对顶角相等),
∴∠AEF=∠AFE,故②正确;
∵∠ABE=∠CBE,
∴只有∠C=30°时∠EBC=∠C,故③错误;
∵∠AEF=∠AFE,
∴AE=AF,
∵AG平分∠DAC,
∴AG⊥EF,故④正确.
综上所述,正确的结论是①②④.
故选C.
【点睛】本题考查了直角三角形的性质,等腰三角形三线合一的性质,同角的余角相等的性质以及等角的余角相等的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.
【14.题】
【答案】C
【解析】根据同位角的概念可知,①中∠1与∠2是同位角,②中∠1与∠2是同位角,③中∠1与∠2不是同位角,④中∠1与∠2不是同位角,⑤中∠1与∠2是同位角,故选C.
【15.题】
【答案】D
【解析】试题分析:根据同位角的概念,两直线被第三条直线所截,两个角在被截线的同旁,在截线的同侧,称为同位角,因此可知D为同位角.
故选:D.
点睛:此题主要考查了“三线八角”的确定,解题关键是明确在两直线被第三条直线所截时,同位角、内错角、同旁内角的确定.
同位角:分别在两条直线的同一侧,并且都在第三条直线的同一旁。
内错角:在两条直线之间,并且分别在第三条直线的两旁。
同旁内角:在两条直线之间,并且都在第三条直线的同一旁。
【16.题】 【答案】C 【解析】A. 经过直线外一点,有且只有一条直线与已知直线垂直,应该强调在同一平面内,如果是空间会有无数条直线与已知直线垂直,故错误; B. 平分弦的直径垂直于弦,应该强调被平分的弦不是直径,故错误; C. 对角线互相平分且垂直的四边形是菱形 ,正确; D. 反比例函数
,当k<0时,y随x的增大而减小,故错误;故选C.
【17.题】 【答案】D 【解析】试题解析:如图,
从点A作直线l的垂线,垂足为C点,当A、B、C三点共线时,线段AB的长为7-3=4cm,其它情况下大于4cm, 故选D.
【18.题】
【答案】D
【解析】试题分析:根据同位角的意义,可知∠A与∠EDC是同位角,故A不正确;
根据内错角的意义,可知∠A与∠ABF是内错角,故B不正确;
根据同旁内角的特点,可知∠A的同旁内角为∠ADC或∠ABC,故C不正确,D不是同旁内角,故正确.
故选:D.
点睛:两直线被第三条直线所截,同位角在截线的同侧,在被截线的同旁,同旁内角是在被截线之间,截线的同侧,内错角在被截线之间,截线的两侧.
【19.题】
【答案】A
【解析】∵CD∥AB,∠B=50°,
∴∠BCD=∠B=50°.
∵BC⊥AE,
∴∠BCE=90°,
∴∠1=90°-∠BCD=90°-50°=40°
故选A.
【20.题】
【答案】B
【解析】①. ∵两条平行直线被第三条直线所截,同位角相等,故不正确;
②. ∵对顶角一定相等,邻补角的和一定为1800,故正确;
③.∵平面直角坐标系把平面上的点分为四部分,故正确;
④. ∵体育老师测定同学的跳远成绩的依据是垂线段最短,故正确;
⑤.在同一平面内,三条直线a,b,c若满足a⊥b,b⊥c,则a∥c.故不正确;
故选B.
【21.题】 【答案】C 【解析】如图,可以有4个;
故选C.
【22.题】 【答案】C 【解析】平行四边形ADCE的对角线的交点是AC的中点O,当OD⊥BC时,OD最小,即DE最小. ∵OD⊥BC,BC⊥AB,∴OD∥AB. 又∵OC=OA,∴OD是△ABC的中位线,
,∴DE=2OD=6.故选C. 【知识拓展】因为点O是定点,由于直线外一点与直线上各点连接的所有线段中垂线段最短,所以当OD⊥BC时,OD最小,即DE最小.
【23.题】
【答案】B
【解析】①相等的角是对顶角,错误;
②同旁内角互补,错误;
③在同一平面内,若a∥b,b∥c,则a∥c,故正确;
④末位是零的整数能被5整除,正确,
故选:B。
点睛:本题考查了命题与定理的知识,解题的关键是了解对顶角的定义、平行线的性质等知识分别判断后即可确定正确的选项.注意:要说明一个没命题的正确性,一般需要推理、论证,二判断一个命题是假命题,只需举出一个范例即可.
【24.题】 【答案】36° 【解析】 试题分析:先根据OF⊥CD,得出∠AOC ∠AOF=90°,再根据∠AOF与∠AOC的度数之比为3:2,列出关于x的方程,求得x的值,进而得出∠AOC的度数. 解:∵OF⊥CD, ∴∠COF=90°, ∴∠AOC ∠AOF=90°, ∵∠AOF与∠BOD的度数之比为3:2, ∴∠AOF与∠AOC的度数之比为3:2, 设∠AOF=3x,∠AOC=2x,则 3x 2x=90°, 解得x=18°, ∴∠AOC=2x=36°.
【点评】本题主要考查了垂线以及对顶角的概念,解决问题的关键是利用角的和差关系进行计算求解.解题时注意运用对顶角的性质:对顶角相等.
【25.题】
【答案】120°
【解析】
试题分析:由OE⊥AB可得∠EOB=90°,设∠COE=x,则∠DOE=5x,而∠COE ∠EOD=180°,即x 5x=180°,得到x=30°,则∠BOC=30° 90°=120°,利用对顶角相等即可得到∠AOD的度数.
解:∵OE⊥AB,
∴∠EOB=90°,
设∠COE=x,则∠DOE=5x,
∵∠COE ∠EOD=180°,
∴x 5x=180°,
∴x=30°,
∴∠BOC=∠COE ∠BOE=30° 90°=120°,
∴∠AOD=∠BOC=120°.
【26.题】
【答案】BOF=38°19′,∠AOF=141°41′.
【解析】
试题分析:因为AB⊥CD,得出∠AOD=∠BOD=90°,再由∠EOD=128°19′,得出∠AOE,求得∠BOF,进一步求出∠DOF,得出∠AOF的度数.
解:∵AB⊥CD,
∴∠AOD=∠BOD=90°,
∴∠BOF=∠AOE=∠EOD﹣∠AOD=128°19′﹣90°=38°19′,
∴∠DOF=∠BOD﹣∠BOF=90°﹣38°19′=51°41′,
∴∠AOF=∠AOD ∠DOF=90° 51°41′=141°41′.
【27.题】 【答案】95m. 【解析】如图,过点A做AD⊥BC于点D,则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°,∠CAD=45°, ∴在Rt△ADC中,CD =AD,
在Rt△ABD中,BD=ADtan30°, ∵BD CD=150 ∴AD ADtan30°=150 即
解得
(m) 答:A点到BC的距离是95 m.
【28.题】 【答案】垂线段最短 【解析】试题分析:作AP⊥直线l于P,连接AB,P就是所求的水泵站的位置. 试题解析:作AP⊥直线l于P,连接AB,如图,P就是所求的水泵站的位置;
依据是垂线段最短和两点之间线段最短. 【点睛】本题考查了作图-应用与设计作图,垂线段最短、两点之间线段最短是本题的关键.
【29.题】 【答案】50°. 【解析】试题分析:根据题意得出∠AOC以及∠AOD的度数,进而结合垂直的定义以及角平分线的性质得出答案. 试题解析:∵∠AOC与∠AOD的度数比为4:5, ∴∠AOC=180°×
=80°,∠AOD=180°×
=100°, ∵OE⊥AB,OF平分∠DOB, ∴∠EOD=10°,∠DOF=
×80°=40°, ∴∠EOF的度数为:10° 40°=50°.
【30.题】 【答案】(1)62°;(2)正确, 【解析】试题分析:(1)根据对顶角相等求出∠AOC的度数,根据垂直的定义计算即可; (2)设∠BOD=x,用x表示出∠AOC和∠BOC,根据邻补角的概念计算即可; 试题解析: (1)∵∠BOD=28°, ∴∠AOC=∠BOD=28°, ∵OE⊥CD, ∴∠EOC=90°, ∴∠AOE=∠EOC﹣∠AOC=62°; (2)正确, 设∠BOD=x,则∠AOC=∠BOD=x,∠BOC=180°﹣x, ∵OF平分∠AOC, ∴∠FOC=
x, ∴∠EOF=90°﹣∠FOC=90°﹣
x, ∴∠EOF=
∠BOC.
【31.题】
【答案】50°.
【解析】试题分析:由已知AB⊥BC,得∠ABC=90°,再由∠ABE=50°可得∠BEC=40°,又因BE∥CF,根据平行线的性质得出∠EBC=∠BCF=40°,再由BC⊥CD可得∠DCF ∠BCF=90°,即可求得∠DCF=50°.
试题解析:
∵AB⊥BC,∴∠ABC=90°.
∵∠ABE=50°,∴∠CBE=90°-50°=40°.
∵BE∥CF,∴∠FCB=∠CBE=40°.
∵BC⊥CD,∴∠DCF ∠BCF=90°.
∴∠DCF=90°-40°=50°
点睛:此题考查了平行线的性质与垂线的定义.此题比较简单,解题的关键是注意掌握两直线平行,内错角相等定理的应用.
【32.题】 【答案】165° 【解析】解:∵∠AOC=30° ∴∠BOC=180°-∠AOC=150° ∵ OF平分∠BOC ∴∠COF=
∠BOC=75° ∵OE⊥CD ∴∠EOC=90° ∴∠EOF ∠EOC ∠∠COF=90° 75°=165°
【33.题】 【答案】作图见解析 【解析】(1)如图: AE就是所求图形 (2)如图: BF就是所求图形
【34.题】 【答案】小淇同学作法正确.理由见解析 【解析】试题分析:小淇同学作法正确.连接OB.由作法可得OA=OC=OB.再由三角形内角和可得∠ABC=90°,从而得AB⊥l. 试题解析:小淇同学作法正确. 理由如下:连接OB. ∵O为AC中点,以O为圆心,OA长为半径画弧交直线l于点B,∴OA=OC=OB. ∴∠CAB=∠ABO,∠ACB=∠CBO,又∵∠CAB ∠ABO ∠ABC ∠CBO=180°,∴∠ABO ∠CBO=90°.∴∠ABC=90°,即AB⊥l.
【35.题】
【答案】(1)∠AOC=58°;(2)30°
【解析】试题分析:(1)根据垂直的定义可得∠COD=90°,再由∠AOB为平角,∠BOD=32°即可求得∠AOC的度数;(2)设∠BOD=x,则∠AOC=2x,根据平角的定义列方程求解即可.
试题解析:
(1)∵OC⊥OD
∴∠COD=90°
∵∠AOB是平角
∴∠AOB=180°
∵∠BOD=32°
∴∠AOC=180°-∠BOD-∠COD=58°
(2)设∠BOD=x,则∠AOC=2x,
∴x 2x 90°=180°,
解得x=30°,即∠BOD=30°.
【36.题】
【答案】①②④.
【解析】
试题分析:在同一平面内,平行于同一条直线的两直线平行;垂直于同一条直线的两直线平行.
考点:平行线的性质.
【37.题】
【答案】连接直线外一点与直线上所有点的连线中,垂线段最短.
【解析】
试题分析:过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.
解:根据垂线段定理,连接直线外一点与直线上所有点的连线中,垂线段最短,
∴沿AB开渠,能使所开的渠道最短.
故答案为:连接直线外一点与直线上所有点的连线中,垂线段最短.
【点评】本题是垂线段最短在实际生活中的应用,体现了数学的实际运用价值.
【38.题】
【答案】53,37.
【解析】
试题分析:根据已知直线AB、CD、EF相交于点O,AB⊥CD,∠DOE=127°,由邻补角互补、对顶角相等,可以求得∠COE和∠AOF的度数.
解:∵∠DOE=127°,∠DOE ∠COE=180°,
∴∠COE=53°,
∵AB⊥CD,
∴∠COB=90°,
∴∠COE ∠BOE=90°,
∴∠BOE=37°,
∵∠BOE=∠AOF,
∴∠AOF=37°,
故答案为:53,37.
【点评】本题考查垂线、对顶角、邻补角,解题的关键是明确题意,灵活变化,找出所求角需要的条件.
【39.题】
【答案】如果两条直线垂直于同一条直线,那么这两条直线平行.
【解析】
试题分析:命题由题设和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项.命题常常可以写为“如果…那么…”的形式,如果后面接题设,而那么后面接结论.
解:把命题“垂直于同一条直线的两直线平行”,改写成“如果…,那么…”的形式:如果两条直线垂直于同一条直线,那么这两条直线平行.
【40.题】
【答案】如果两个角是对顶角,那么它们相等
【解析】
试题分析:命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.
解:题设为:对顶角,结论为:相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么它们相等,
故答案为:如果两个角是对顶角,那么它们相等.
【41.题】 【答案】32° 【解析】 试题分析:首先根据角平分线的定义求得∠BOD,然后根据对顶角相等即可求解. 解:∵OB平分∠DOE, ∴∠BOD=
∠DOE=32°, ∴∠AOC=∠BOD=32°. 故答案是:32°.
【42.题】
【答案】45
【解析】
试题分析:根据补角和余角的定义列式计算.
解:设这个角为α,则它的补角为180°﹣α,余角为90°﹣α,
根据题意(180°﹣α):(90°﹣α)=3:1,
解得α=45°.
故答案为45.
【43.题】
【答案】48°
【解析】试题解析:∵OE⊥AB,∠EOD=42°,
∴∠BOD=90°-∠EOD=90°-42°=48°,
∵∠BOD与∠AOC是对顶角,
∴∠BOD=∠AOC=48°.
【44.题】
【答案】AB
【解析】试题解析:点到直线的距离就是这一点到直线的垂线段的长度,所以是线段AB的长.
【45.题】 【答案】2 【解析】当DE
BC时,线段DE有最小值, ∵BD平分∠ABC,∠A=900, ∴DE=AD 又∵AD=2, ∴DE=2; 故答案是:2。
【46.题】
【答案】垂线段最短
【解析】根据垂线的性质可得,小丽选择了家与河岸垂直的路线是因为垂线段最短.
【47.题】
【答案】75°
【解析】∵OC⊥OD,
∴∠COD=90°.
∴∠AOC ∠BOD=90°
设∠BOD为x,则∠AOC为5x.
根据题意得:x 5x=90°,
解得:x=15°.
∴∠AOC=5x=75°.
故答案为:75°.
【48.题】 【答案】
和
【解析】试题分析:根据对顶角相等可知∠AOC=∠BOD,∠DOF=90°,可根据和为180°的两角互为补角,可知∠COE的补角为∠EOD何∠BOF.
【49.题】 【答案】线段
的长度 【解析】试题分析:根据点到直线的距离为点到直线的垂线段的长度,可知CD的长度为点C到AB的距离. 故答案为:CD的长度
【50.题】 【答案】(1)AB∥CD;(2)证明见解析;(3)
角度不会发生改变,理由见解析. 【解析】试题分析:(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补,所以易证AB∥CD; (2)利用(1)中平行线的性质推知°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件GH⊥EG,易证PF∥GH; (3)利用三角形外角定理、三角形内角和定理求得∠4=90°-∠3=90°-2∠2;然后由邻补角的定义、角平分线的定义推知∠QPK=
∠EPK=45° ∠2;最后根据图形中的角与角间的和差关系求得∠HPQ的大小不变,是定值45°. 试题解析:(1)如图1,
∵∠1与∠2互补, ∴∠1 ∠2=180°. 又∵∠1=∠AEF,∠2=∠CFE, ∴∠AEF ∠CFE=180°, ∴AB∥CD; (2)如图2,
由(1)知,AB∥CD, ∴∠BEF ∠EFD=180°. 又∵∠BEF与∠EFD的角平分线交于点P, ∴∠FEP ∠EFP=
(∠BEF ∠EFD)=90°, ∴∠EPF=90°,即EG⊥PF. ∵GH⊥EG, ∴PF∥GH; (3)∠HPQ的大小不发生变化,理由如下: 如图3,
∵∠1=∠2, ∴∠3=2∠2. 又∵GH⊥EG, ∴∠4=90°-∠3=90°-2∠2. ∴∠EPK=180°-∠4=90° 2∠2. ∵PQ平分∠EPK, ∴∠QPK=
∠EPK=45° ∠2. ∴∠HPQ=∠QPK-∠2=45°, ∴∠HPQ的大小不发生变化,一直是45°. 【点睛】本题考查了平行线的判定与性质.解题过程中,注意“数形结合”数学思想的运用.
,