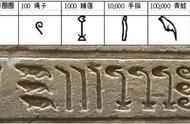
七年级数学下册的第八章,就开始学二元一次方程了。作为中考数学的必考知识点,二元一次方程在考试中的分数占比也是非常高的。想要学好二元一次方程,我们就要掌握解方程的几种思路,本期就跟大家分享9种解二元一次方程的思路。建议收藏。

整体代入法是用含未知数的表达式代入方程进行消元。有些方程组并不一定能直接应用这种解法,不过,我们可以创造条件进行整体代入。

解析:这道题中的系数较繁,按常规方法去解比较麻烦.我们可以先将②式有目的地进行变形,再将①式中的看成一个整体代入求解。由②式可得化简,得③将①代入③,得。解得,代入①可得。
二、换元法换元法就是设出一个辅助未知数,分别用含有这个未知数的代数式表示原方程组中未知数的值,把二元一次方程组转化为一元一次方程组进行求解。换元有一定的技巧性。有代数式整体换元,还有设比值换元等多种方法。

解析:换元法多用于式子较多,有分数的二元一次方程中。通过换元法把繁杂的式子,换元法多用于式子较多,有分数的二元一次方程中。通过换元法把繁杂的式子变成简洁易懂的一次方程,解起来就简单多了。
三、直接加减法直接加减法有别于课本中的加减消元法,它通过将方程组中的方程相加减后把较繁的题目转化得相对简单。