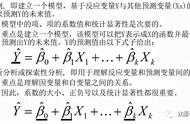如果函数有二阶导数,那么如果函数二阶导数为正,或者对于多元函数,Hessian矩阵半正定则为凸函数。
(也可能引到SVM,或者凸函数局部最优也是全局最优的证明,或者上述公式期望情况下的Jessen不等式)
8、如何解决类别不平衡问题?
有些情况下训练集中的样本分布很不平衡,例如在肿瘤检测等问题中,正样本的个数往往非常的少。从线性分类器的角度,在用

对新样本进行分类的时候,事实上在用预测出的y值和一个y值进行比较,例如常常在y>0.5的时候判为正例,否则判为反例。几率

反映了正例可能性和反例可能性的比值,阈值0.5恰好表明分类器认为正反的可能性相同。在样本不均衡的情况下,应该是分类器的预测几率高于观测几率就判断为正例,因此应该是

时预测为正例,这种策略称为rebalancing。但是训练集并不一定是真实样本总体的无偏采样,通常有三种做法,一种是对训练集的负样本进行欠采样,第二种是对正例进行升采样,第三种是直接基于原始训练集进行学习,在预测的时候再改变阈值,称为阈值移动。注意过采样一般通过对训练集的正例进行插值产生额外的正例,而欠采样将反例划分为不同的集合供不同的学习器使用。
9、解释对偶的概念。
一个优化问题可以从两个角度进行考察,一个是primal 问题,一个是dual 问题,就是对偶问题,一般情况下对偶问题给出主问题最优值的下界,在强对偶性成立的情况下由对偶问题可以得到主问题的最优下界,对偶问题是凸优化问题,可以进行较好的求解,SVM中就是将primal问题转换为dual问题进行求解,从而进一步引入核函数的思想。
10、如何进行特征选择?
特征选择是一个重要的数据预处理过程,主要有两个原因,首先在现实任务中我们会遇到维数灾难的问题(样本密度非常稀疏),若能从中选择一部分特征,那么这个问题能大大缓解,另外就是去除不相关特征会降低学习任务的难度,增加模型的泛化能力。冗余特征指该特征包含的信息可以从其他特征中推演出来,但是这并不代表该冗余特征一定没有作用,例如在欠拟合的情况下也可以用过加入冗余特征,增加简单模型的复杂度。
在理论上如果没有任何领域知识作为先验假设那么只能遍历所有可能的子集。但是这显然是不可能的,因为需要遍历的数量是组合爆炸的。一般我们分为子集搜索和子集评价两个过程,子集搜索一般采用贪心算法,每一轮从候选特征中添加或者删除,分别成为前向和后先搜索。或者两者结合的双向搜索。子集评价一般采用信息增益,对于连续数据往往排序之后选择中点作为分割点。
常见的特征选择方式有过滤式,包裹式和嵌入式,filter,wrapper和embedding。Filter类型先对数据集进行特征选择,再训练学习器。Wrapper直接把最终学习器的性能作为特征子集的评价准则,一般通过不断候选子集,然后利用cross-validation过程更新候选特征,通常计算量比较大。嵌入式特征选择将特征选择过程和训练过程融为了一体,在训练过程中自动进行了特征选择,例如L1正则化更易于获得稀疏解,而L2正则化更不容易过拟合。L1正则化可以通过PGD,近端梯度下降进行求解。
11、为什么会产生过拟合,有哪些方法可以预防或克服过拟合?
一般在机器学习中,将学习器在训练集上的误差称为训练误差或者经验误差,在新样本上的误差称为泛化误差。显然我们希望得到泛化误差小的学习器,但是我们事先并不知道新样本,因此实际上往往努力使经验误差最小化。然而,当学习器将训练样本学的太好的时候,往往可能把训练样本自身的特点当做了潜在样本具有的一般性质。这样就会导致泛化性能下降,称之为过拟合,相反,欠拟合一般指对训练样本的一般性质尚未学习好,在训练集上仍然有较大的误差。
欠拟合:一般来说欠拟合更容易解决一些,例如增加模型的复杂度,增加决策树中的分支,增加神经网络中的训练次数等等。
过拟合:一般认为过拟合是无法彻底避免的,因为机器学习面临的问题一般是np-hard,但是一个有效的解一定要在多项式内可以工作,所以会牺牲一些泛化能力。过拟合的解决方案一般有增加样本数量,对样本进行降维,降低模型复杂度,利用先验知识(L1,L2正则化),利用cross-validation,early stopping等等。
12、什么是偏差与方差?
泛化误差可以分解成偏差的平方加上方差加上噪声。偏差度量了学习算法的期望预测和真实结果的偏离程度,刻画了学习算法本身的拟合能力,方差度量了同样大小的训练集的变动所导致的学习性能的变化,刻画了数据扰动所造成的影响,噪声表达了当前任务上任何学习算法所能达到的期望泛化误差下界,刻画了问题本身的难度。偏差和方差一般称为bias和variance,一般训练程度越强,偏差越小,方差越大,泛化误差一般在中间有一个最小值,如果偏差较大,方差较小,此时一般称为欠拟合,而偏差较小,方差较大称为过拟合。
偏差: