lr模型的基本原理,lr测试入门

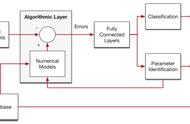
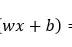逻辑回归是个看似简单又在面试中常常被问到的机器学习算法，虽然表面上看起来很简单，容易掌握，但真正问到细节时卡住，在某些点上还是容易卡住的。

所以，给大家的建议是在面试时，如果面试官让你说一个自己最精通的机器学习算法，那么建议大家不要直接说自己精通逻辑回归，因为十分容易被问到，从而减分。

推荐大家将 SVM 算法作为自己的第一个算法去讲解，因为 SVM 没有那么多小细节，只要掌握了就不容易掉坑里。下面总结一下面试中逻辑回归的常见考点。

逻辑回归是在数据服从伯努利分布的假设下，通过极大似然的方法，运用梯度下降法来求解参数，从而达到将数据二分类的目的。

将数据进行二分类

逻辑回归作为一个回归函数，如何用于分类问题。 逻辑回归中，对于每个 x，其条件概率 y 的确是一个连续的变量。而逻辑回归中可以设定一个阈值，y 值大于这个阈值的是一类，y 值小于这个阈值的是另外一类。至于阈值的选择，通常是根据实际情况来确定，一般情况下选取 0.5 作为阈值来划分。

（1）数据服从伯努利分布。 一个简单的伯努利分布的例子就是抛硬币，假设硬币被抛出正面的概论为 p，被抛出负面的概论为 1-p，则这些硬币抛出的正负两面所代表的随机变量即服从伯努利分布。

（2）假设样本为正的概论 p 为一个 Sigmoid 函数。 为什么要使用 Sigmoid 函数，事实上，设计一个分类模型，首先需要给它设定一个学习目标，即通过优化一个损失函数来求解参数。那么，在逻辑回归中，这个目标就是最大化似然度。

考虑一个二值分类问题，训练数据是一堆（特征，标记）组合，(x1, y1)，(x2, y2)，... 其中 x 是特征向量，y 是类标记（y = 1 表示正类，y = 0 表示反类）。

LR 首先定义一个条件概率 p(y | x; w)。p(y | x; w) 表示给定特征 x ，类标记 y 的概率分布，其中 w 是 LR 的模型参数（一个超平面）。有了这个条件概率，就可以在训练数据上定义一个似然函数，然后通过最大似然来学习 w，这是 LR 模型的基本原理。

那么如何定义这个条件概率呢，我们知道，对于大多数线性分类器，response value（响应值）<w, x> （w 和 x 的内积） 代表了数据 x 属于正类（y = 1）的 confidence（置信度）。

<w, x> 越大，这个数据属于正类的可能性越大；<w,x> 越小，属于反类的可能性越大。

<w, x> 在整个实数范围内取值。现在我们需要用一个函数把 <w, x> 从实数空间映射到条件概率 p(y = 1 | x, w) 上，并且希望 <w, x> 越大，p(y = 1 | x, w) 越大；<w, x> 越小，p(y = 1 | x, w) 越小，而 Sigmoid 函数恰好能实现这一功能：首先，它的值域是 (0，1)，满足概率的要求；其次，它是一个单调上升函数。最终，p(y = 1 | x, w) = Sigmoid(<w, x>)。

逻辑回归的损失函数是其极大似然函数。

极大似然函数无法直接求解，一般是通过对该函数进行梯度下降来不断逼近其最优解。这里需要注意的点是要对梯度下降有一定的了解，就梯度下降本身来看的话就有随机梯度下降，批梯度下降，small batch 梯度下降三种方式，面试官可能会问这三种方式的优劣以及如何选择最合适的梯度下降方式。

• 批梯度下降会获得全局最优解，缺点是在更新每个参数的时候需要遍历所有的数据，计算量会很大，并且会有很多的冗余计算，导致的结果是当数据量大的时候，每个参数的更新都会很慢。
• 随机梯度下降是以高方差频繁更新，优点是使得 sgd 会跳到新的和潜在更好的局部最优解，缺点是使得收敛到局部最优解的过程更加的复杂。
• 小批量梯度下降结合了批梯度下降和随机梯度下降的优点，每次更新的时候使用 n 个样本。减少了参数更新的次数，可以达到更加稳定收敛结果，一般在深度学习当中我们采用这种方法。

对于逻辑回归，这里所说的对数损失和极大似然是相同的。 不使用平方损失的原因是，在使用 Sigmoid 函数作为正样本的概率时，同时将平方损失作为损失函数，这时所构造出来的损失函数是非凸的，不容易求解，容易得到其局部最优解。 而如果使用极大似然，其目标函数就是对数似然函数，该损失函数是关于未知参数的高阶连续可导的凸函数，便于求其全局最优解。

优点：

• 形式简单，模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大。
• 模型效果不错。在工程上是可以接受的（作为 baseline），如果特征工程做的好，效果不会太差，并且特征工程可以并行开发，大大加快开发的速度。
• 训练速度较快。分类的时候，计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化 SGD 发展比较成熟。
• 方便调整输出结果，通过调整阈值的方式。

缺点：

• 准确率欠佳。因为形式非常的简单，而现实中的数据非常复杂，因此，很难达到很高的准确性。
• 很难处理数据不平衡的问题。举个例子：如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1。我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器，它对正负样本的区分能力不会很好。
• 无法自动的进行特征筛选。
• 只能处理二分类问题。

损失函数：线性模型是平方损失函数，而逻辑回归则是似然函数。

如果在损失函数最终收敛的情况下，其实就算有很多特征高度相关也不会影响分类器的效果。 但是对特征本身来说的话，假设只有一个特征，在不考虑采样的情况下，你现在将它重复 N 遍。训练以后完以后，数据还是这么多，但是这个特征本身重复了 N 遍，实质上将原来的特征分成了 N 份，每一个特征都是原来特征权重值的百分之一。

1. 去掉高度相关的特征会让模型的可解释性更好；
2. 可以大大提高训练的速度。