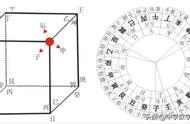
托勒密定理:圆内接四边形两条对角线的乘积等于两对对边乘积之和。
托勒密定理的证明:
已知:四边形ABCD内接于圆,如图,求证:AB·CD BC·AD=AC·BD.

证明:在∠BAD内作∠BAE=∠CAD,交BD于E。因∠ABE=∠ACD,所以△ABE∽△ACD,从而AB·CD =AC·BE ①;
易证△ADE∽△ACB,所以BC·AD=AC·DE ②;
1 ②得AB·CD BC·AD=AC·BD。
例2.蝴蝶定理
已知:过圆O的弦PQ的中点M任作两条相交弦AB、CD,联结AC、BD分别与PQ交于E和F。

求证:ME=MF.
根据维基百科,此结论1803年被提出,1944年被命名为蝴蝶定理,确实本图形形状酷似一只翩翩起舞的蝴蝶。此题图形简洁、结论优美,证明却殊为不易。所以此题一经披露,就引起了众多关注,也出现了多种证明,常见的有10多种。最早见于1815年《男士日记》,近年来,此定理又载沉载浮,出现了一些新的证明,分蘖出新的变种,并在竞赛及练习中时隐时现。本系列文章准备系统梳理此定理的经典证明,挖掘其本质,详细介绍各种变式,并结合最新题目展示其应用。第一篇文章准备先介绍本定理的五种典型证法。
本定理证明的思路主要是两类:一类是纯几何方法,另一类是计算。计算方法又大概分为两类:三角计算(面积法、Menelaus定理、交比等)、解析法。
纯几何方法一
思路分析1:看到圆及中点M想到垂径定理,两边元素相对分散,考虑到将C关于OM对称到C',倒角发现MBC'F共圆,然后利用全等即可。

证明1:作弦CC'∥PQ,联结C'M、C'F。
则C、C'关于OM对称,故∠FMC'=∠MC'C=∠MCC'=∠DBC',故M、B、C'、F四点共圆,故∠F C'M=∠ABD=∠ECM,
又CM=C'M, ∠FMC'=∠EMC,则△CME≌△C'MF(ASA),故ME=MF。
纯几何方法二
思路分析2:显然OM⊥PQ,欲证ME=MF,即证△OME≌△OMF。显然△AMC∽△DMB,由对称性想到垂径定理,取AC、BD中点,从而得到共圆及等角,即得证。