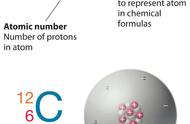
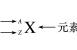(一)放射性同位素的应用:定年
所谓定年,就是利用放射性同位素衰变的性质,测定体系不与外界发生同位素交换后的年龄。
就像可以通过判断发量估算博士生的年级一样。如果假定读博之前的发量为固定值,随着读博时间的增加,发量以一个固定的速率减小,就可以通过目前的发量与初始发量的比值来推测读博的时间。(X)

对于同位素定年也是相似的,体系不与外界发生同位素交换时可以看作“入学“,而同位素母体随着时间逐渐衰变减少,就像头发一样。那么我们只要测定样品中剩余母体的含量(当前发量),并通过一些方式估计出初始母体的含量(初始发量),由于同位素衰变的半衰期(发量减少速率)是已知的,那么我们就可以得到所测样品不与外界发生交换多少年了,从而得到了样品的”年龄”。
比如我们熟悉的碳-14定年,就是测定体系不与外界发生碳同位素的交换后的年龄。
由于宇宙射线的作用,在大气中会发生核反应生成碳-14,通常认为这一速率大致不变;同时碳-14发生衰变,那么大气中的碳-14就会在生成和衰变中达到一定的稳态,最终大气中碳-14含量基本不变。木材砍伐并制成棺木后,其中的碳将不再与大气发生交换,此后碳-14发生衰变,以一定的速率减少。我们通过测量棺木中的碳-14含量,将其与大气中的碳-14含量对比,又已知衰变速率,就可以知道棺木是什么年代的产物了。

对于其他的放射性同位素定年方式,原理也比较相似,只不过要根据不同的时间尺度选择不同的同位素体系。
如果选用的半衰期过短,那么样品中的母体含量就会很少,于是甚至测量不出来;如果选用的半衰期过长,那么母体含量几乎没有变化,也不能定出年龄。
例如地球的年龄就要通过U-Pb体系来确定。
对于同位素定年,其中比较关键的一点是对于初始含量估计。因为大多数情况下我们并不知道放射性母体的初始含量,所以我们需要通过很多其他的方式来假定母体的含量或通过公式的转换,将初始母体的含量变成其他可以确定的量。其中比较常用的有模式年龄法、等时线法等。

等时线法
(二)稳定同位素的应用:测温、示源、示踪
对于稳定同位素的应用,则主要是利用了同一元素的同位素的性质既具有相似性又具有差异性的特点。就像W.M.White在其所编教材Geochemistry中所言,Thus is it that one group of isotope geochemists make their living by measuring isotope fractionations while the other group makes their living by ignoring them!(一群同位素地球化学家靠着测量同位素的分馏而生存,而另一群则靠的是忽略同位素的分馏)