现在我们复习平面向量的加法运算,同学们都知道向量加法的运算是向量运算的重要基础,所以我们必须理解和掌握向量加法的意义和运算法则。
一、平面向量的加法运算重点要理解和掌握以下几点
1、平面向量加法运算的意义
求两个向量和的运算叫做向量的加法运算。
2、平面向量的写法与读法
同学们注意表示向量的字母有两种写法,一种是用小写字母a或b,读做向量a、b。第二种是用大写字母表示向量,例如用AB头上要加一条横线段,线段的右端加上箭头(下文简称横线)表示向量,读做向量AB。我们在这里不能写出AB头上的横线,只能用AB代替向量,AB头上加横线的写法,下文向量的标准写法在这里简写为a、b或AB。希望同学们平时不要误写,平面向量的写法和读法要以现行教材为准。
另外有的图形因个人的水平有限在这里不能画出,希望同学们结合教材中的图形来阅读这个复习稿。
3、平面向量加法的运算法则
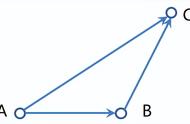
(一)、三角形法则
我们看到已知非零向量a,b在平面内任取一点A,作向量AB=a,BC=b。则向量AC叫做a与b的和,记作a b,即
a b=AB BC=AC
这种求向量和的方法,叫做向量加法的三角形法则。同学们自己把这个图形画出来。
注意以下几点:
1、向量加法的三角形法则适用于向量首尾相接的情况。
2、向量加法的三角形法则,可以推广到两个以上的非零向量相加。特别的向量
AB B1B2 B2B3
…Bn-1Bn=ABn
(二)、平行四边形法则
以同一点O为起点的两个已知向量a,b为邻边作平行四边形
OACB,则以O为起点的对角线OC就是a与b的和,把这种作两个向量和的方法叫做向量加法的平行四边形法则。
我们再深入探讨
1、当两个向量不共线时,向量加法的三角形法则和平行四边形法则是一致的。
2、对于零向量与任一向量a,我们规定a 0=0 a=a。
3、平行四边形法则适用于向量有共同的起点
(三)、向量加法的运算定律
1、交换律:a b=b a
2、结合律:(a b) c=a (b c)
(四)、我们拓展深化进行探讨
1、两个向量的和仍然是一个向量
2、对于任意向量a、b则有
|a b丨<或=丨a丨 丨b丨
当a//b时
丨a b丨=丨a丨 丨b丨
当a,b反向或a、b中至少有一个为0时,丨a b丨=|a丨-丨b丨
或丨b丨-丨a丨
关于平面向量的加法运算的意义和运算法则,我们就复习到这里。因参考资料的版本不同,在复习中有争议的地方或打字排版出现错误的地方,要以现行教材为准,也希望审核老师和同学们批评指正。谢谢!
作业与要求
把现行教材中平面向量加法运算的练习题,用练习本全部作完。