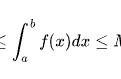今天是高等数学专题的第12篇,我们继续来看定积分。
之前在讲微分求导内容的时候,介绍过一系列微分中值定理的推导。既然有微分中值定理,那么自然也有积分中值定理,我们下面就来看看积分中值定理的定义。
极值定理
极值定理也叫最大最小值定理,它的含义非常直观:如果函数f(x)在区间[a,b]上连续的函数,必然存在最大值和最小值,并且取到最大值和最小值至少一次。
这是一个非常有名的定理,定理的内容很直观,也不难理解。但是证明它不太容易,是由区间套定理与B-M定理等多个定理推导得到的,这段证明过程比较复杂,由于篇幅和水平的限制,本文当中只能跳过这部分,感兴趣的同学可以自行了解。
我们假设m和M分别是区间[a, b]上函数f(x)的最小值和最大值,那么根据极值定理,可以得到以下式子成立:

这个式子光看可能会觉得有些复杂,但是我们把图画出来之后非常简单:

上图当中灰色阴影部分就是定积分的结果,蓝色的矩形面积是m(b-a),大的矩形面积是M(b-a)。
通过几何面积的关系我们可以很容易证明结论。
数学证明也很简单,由于m和M分别是最小值和最大值,所以我们可以得到 m <= f(x) <= M。我们把常数也看成是函数,进行积分,于是可以得到:

两边积分的结果就是矩形面积,于是我们就得到了证明。
积分中值定理
极值定理非常简单,但是是很多定理的基础,比如我们的积分中值定理就和它密切相关。
我们对上面的式子做一个简单的变形,由于b-a是常数并且大于0,所以我们在