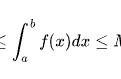搞明白这些细节之后,我们再来看刚才的式子:

我们再把常数乘回来:

右边的积分算的是什么,算的是函数围成的曲形的面积,但是现在我们转化成了一个函数值乘上了宽,所以我们可以把它看成是矩形的高,我们来看下下面这张图。

也就是说以 f(ξ) 为高的矩形面积和函数围成的曲形面积相等,所以它既是矩形的高,也真的是函数在[a, b]上的平均值。
总结
中值定理是微积分领域当中最重要的定理,几乎没有之一,也是整个微积分搭建起来的脉络。我们熟悉中值定理的推导过程,对于我们对加深对于微积分的理解非常有帮助。更重要的一点是,相对来说,这两个定理的推导过程都不是很难,而且还蛮有意思的,所以推荐大家都亲自上手试一试。
今天的文章就是这些,如果觉得有所收获,请顺手点个关注或者转发吧,你们的举手之劳对我来说很重要。