2. 2. 2 二维坐标系间的转换
在实际的工作中,尤其在在工程测量方面,使用的坐标系都为以高斯- 克吕格投影方法建立的平面直角坐标系,平面直角坐标系是一个二维坐标系,与之对应的高程是通过水准测量的方法获得。二维坐标系间的转换多采用赫尔默特模型[5],赫尔默特模型是一种二维四参数转换模型,其形式如下:

式中,X',Y'为平移量; a 为旋转量; K 为尺度变形因子。式( 7) 也即是:

这里特别说明一点: 赫尔默特相似变换与大家熟知的布尔莎七参数相似变换具备相同的模型但却有质的不同。首先从概念上讲赫尔默特相似变换的旋转参数描述的是坐标框架的旋转,布尔莎转换是位置矢量转换旋转,参数描述的是一个点参考于一个固定坐标框架的旋转。其次在赫尔默特相似变换中点围绕坐标轴逆时针旋转而在布尔莎转换中是顺时针的。值得注意的是国内诸多文献都存在概念上的混淆把布尔莎模型与赫尔默特模型等同起来。在实际应用中如果不注意两种模型的区别必然会出现严重的错误[6]。
3、利用地理信息软件进行坐标转换
3. 1 常见的地理信息数据的格式,见表1

3. 2 坐标数据转换
3. 2. 1 Coord 软件
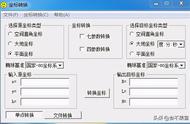
Coord 软件三维七参数转换的步骤为[8]:
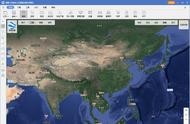
( 1) 投影设置,设置投影方式,以及中央子午线等其他参数;
( 2) 计算七参数,依次将具有两套坐标的控制点( 3 个以上) 输入列表中。输入正确后,选择转换模型为“布尔莎”,计算出七参数。确认后软件将刚才计算的七参数设置为当前值,并保存计算的七参数,( 保存时要注意将转换界面中的源坐标系统和目标坐标系统设置正确,计算七参数时以源坐标为大地坐标,目标坐标为平面直角坐标计算较为方便。) 选择“导出”后弹出对话框供核对,确认后关闭。
( 3) 坐标转换,勾选“七参数转换”,这时可以选择“单点转换”或“文件转换”完成转换。转换的精度见表2。
3. 2. 2 科傻( Cosa) 软件
科傻( Cosa) 软件三维七参数转换步奏如下:
( 1) 首先在“数据处理/设置”对话框中选择相应的椭球参数和中央子午线,
( 2) 将需要转换的坐标转换为空间直角坐标( 如果为平面直角坐标,在Cosa 中则应如下转换: 平面直角→大地坐标→空间直角坐标) ;
( 3 ) 建立一个文本文件,将文件后缀改为* . XYZXYZ,将公共点和待转换点按如下方式编辑:公共点: 点名_X 旧_Y 旧_ Z 旧_ X 新_ Y 新_ Z新; 接着是待转换的点: 点名_X 旧_ Y 旧_ Z 旧;
( 4) 选取“坐标转换”菜单的子项“XYZ→XYZ”,屏幕将出现“打开文件”窗口,选择文件( *. XYZXYZ) 。
( 5) 转换结果保存到文件* . XYZXYZ_0 中。
( 6) 利用记事本将* . XYZXYZ_0 文件打开就可以看到转换后的结果了。转换的精度见表2。