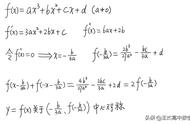【考试要求】
1.结合具体实例,了解y=Asin(ωx+φ)的实际意义;能借助图象理解参数ω,φ,A的意义,了解参数的变化对函数图象的影响;
2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型.
【知识梳理】
1.用五点法画y=Asin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示.


4.三角函数应用
(1)用正弦函数可以刻画三种周期变化的现象:简谐振动(单摆、弹簧等),声波(音叉发出的纯音),交变电流.
(2)三角函数模型应用题的关键是求出函数解析式,可以根据给出的已知条件确定模型f(x)=Asin(ωx+φ)+k中的待定系数.
(3)把实际问题翻译为函数f(x)的性质,得出函数性质后,再把函数性质翻译为实际问题的答案.
【微点提醒】
1.由y=sin ωx到y=sin(ωx+φ)(ω>0,φ>0)的变换:向左平移个单位长度而非φ个单位长度.
2.函数y=Asin(ωx+φ)的对称轴由ωx+φ=kπ+(k∈Z)确定;对称中心由ωx+φ=kπ(k∈Z)确定其横坐标.
3.音叉发出的纯音振动可以用三角函数表达为y=Asin ωx,其中x表示时间,y表示纯音振动时音叉的位移,表示纯音振动的频率(对应音高),A表示纯音振动的振幅(对应音强).
4.交变电流可以用三角函数表达为y=Asin(ωx+φ),其中x表示时间,y表示电流,A表示最大电流,表示频率,φ表示初相位.