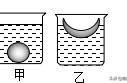
浮力真的与深度和物体密度无关吗?
物体在液体中所受浮力的大小,只跟它排开液体体积和液体的密度有关,与物体本身的密度、运动状态、浸没在液体中的深度等因素无关。
这是中学物理实验中验证过的,再看看试验的操作,如下:
【设计实验】取弹簧测力计、体积相同的铁球和铜球、盛有相同体积盐水和水的烧杯,利用称重法测量不同情况下铁球和铜球受到的浮力。
【进行实验与收集数据】
(1)浮力的大小跟物体浸没在液体中的深度的关系
使用弹簧测力计测出铁球的重力和完全浸没在相同液体中的不同深度时的示数,并记录数据。可以发现,弹簧测力计示数几乎不变。
实验结论1:浮力的大小跟物体浸没在液体中的深度无关。
(2)浮力的大小跟物体浸在液体中的体积的关系
使用弹簧测力计测出铁球的重力和浸在相同液体中体积不同时的示数,并记录数据。可以发现,弹簧测力计示数随浸没在液体中的体积改变而改变。
实验结论2:浮力的大小跟物体浸在液体中的体积有关。物体浸在液体中的体积越大,物体所受的浮力就越大。
(3)浮力的大小跟液体的密度的关系
使用弹簧测力计测出铁球的重力和浸没在密度不同的液体中时的示数,并记录数据。(注意:实验时要使铁球浸没的深度相同)可以发现,物体浸没在密度不同的液体中,弹簧测力计示数不同。
可得出以下实验结论:浮力的大小跟液体的密度有关。液体的密度越大,物体所受浮力就越大。
(4)浮力的大小跟物体的密度的关系
使用弹簧测力计分别测出体积相同的铜球和铁球的重力以及浸没在水中时的示数,并记录数据。(注意:实验时要使铜球和铁球浸没的深度相同)可以发现,铜球和铁球的拉力虽然不同,但F浮=G-F拉相同。
可得出以下实验结论:浮力的大小跟物体的密度无关。
【实验结论】物体在液体中所受的浮力的大小,只跟它浸在液体中的体积和液体的密度有关。物体浸在液体中的体积越大、液体的密度越大,物体所受的浮力就越大。
以上是关于浮力试验的一般操作以及验证的结论。
但是在实际情况中,鱼可以通过鱼鳔调节来保持悬停 ,潜艇下潜需要加重上浮需要减重,船有载重量和吃水深度一说,这些都和水的压强也可以说是深度紧密相关,深度越深水的压强越大,重量越大水的压强也越大,毕竟水是由重力造成的,这些情况好像与上面的试验及结论有点不那么吻合。到底怎么回事呢?
让我们回过头看看上面的四个试验,这四个试验中(2)和(3)其实可以理解为同一个原理的试验,因为在(3)中密度更大的液体浮力越大,可以理解为密度更大液体重量更大,那么效果和(2)中增加水的重量(体积)是一样的,重量增加浮力增大,所以(2)和(3)两个试验的结果一致,也与实际情况吻合;而(1)在原理上和(2)也是一样的,因为深度增加的理解有两种,第一种:可以加水使在面积不变的情况下增加水的深度,第二种:就像(1)的试验中做的一样,通过下沉达到更深的深度,但效果是一致的:增加水的压强。所以(1)和(2)的试验和结论应该也要一致才对。最后是(4),其实(4)可以看做是(1)的过程,因为在(1)中你可以用铁球也可以用铜球。由此可见,上面的这四个试验应该得到同样的结果,但为什么不同呢?从描述看(1)和(4)都是完全浸入水中的,而不是漂浮,那可以认为是悬浮的吗?描述里没有说铁球或铜球是否为悬浮,暂且认为是,但是也没说有什么前提条件,比如说球要超过某个深度。
这个时候或许我要被骂了,那么还是让我继续吧。
用上一篇文章中的图和公式,如下:

图1.物体A漂浮于水上,入水部分为厚度物体的2/3即2a/3,水池的面积为S,物体体积为VA,物体截面尺寸为:a×b,长为c
如图1.物体漂浮于水池的水面上,则物体浮力的计算如下:
物体底部受到的压力为:
2a/3深处水的压力为:
F2a/3=ρ水×g×S×2a/3;
F2a/3-= F2a/3/ S=ρ水×g×2a/3;
F2a/3——水在2a/3处的压力;
F2a/3-——水在2a/3处的平均压力;则:
F物体底= F2a/3-×SA= ρ水×g×b×c×2a/3;
F物体底——物体A水在2a/3处受到的浮力(压力);
SA——物体A底部或顶部面积,SA= b×c;
物体漂浮于水面上,则有:
F物体底=ρ水×g×b×c×2a/3=ρ物×g×VA=MA,则:
ρ水×b×c×2a/3=ρ物×VA,则:
ρ水×S×2a/3=ρ物×VA,令H=2a/3,则有:
ρ水×S×H=ρ物×VA,公式中ρ水、S和VA三个量不变,则有:
当ρ物增大时H增大,而H=2a/3是物体的入水深度,那就意味着ρ物增大时物体的入水深度H增大了,物体受到的压力(浮力)就会增大;当ρ物减小时H也减小,而H=2a/3是物体的入水深度,那就意味着ρ物减小时物体的入水深度减小了,物体受到的压力(浮力)就会减小。当然,以上变化的前提是物体一直漂浮在水面。可见当物体的几何尺寸不变,物体受到的浮力与物体的密度紧密相关(漂浮于水中的物体受到的压力(浮力)随着物体重量的增加而增加,就像空船与船满载的道理一样。),或者说物体的浮力与物体的密度紧密相关,注意这是物体密度不是物质密度。
当物体完全浸没并悬浮于水中时,如下图:

图2.除了假设物体悬浮于水中外其他与图1相同
物体顶部受到的压力为:
H1深处水的压力为:
FH1=ρ水×g×S×H1;
FH1-= FH1/ S=ρ水×g×H1;
FH1——水在H1处的压力;
FH1-——水在H1处的平均压力;
则在H1处:
F物体顶= FH1-×SA=ρ水×g×b×c×H1;
SA——物体A底部或顶部面积,SA= b×c;
物体底部受到的压力为:
H1 a深处水的压力为:
FH1 a=ρ水×g×S×(H1 a);
FH1 a-= FH1 a/ S=ρ水×g×(H1 a);
FH1 a——水在H1 a处的压力;
FH1 a-——水在H1 a处的平均压力;
则在H1 a处:
F物体底= FH1 a-×SA=ρ水×g×b×c×(H1 a);
SA——物体A底部或顶部面积,SA= b×c;
则物体A受到的压力的合力(浮力)为:
F物体= F物体底- F物体顶=ρ水×g×b×c×(H1 a)-ρ水×g×b×c×H1=ρ水×g×b×c×a=ρ水×g×VA;
VA= b×c×a;
F物体——物体A水在顶面距离水面H1处受到的浮力;
VA——物体A的体积。则有:
当物体在顶面距水面H1处悬停时有:
F物体= F物体底- F物体顶=ρ水×g×b×c×(H1 a)-ρ水×g×b×c×H1=ρ水×g×b×c×a=ρ水×g×VA=ρ物×g×VA,则:
ρ水=ρ物;
以上可知此时H1 a处水的密度等于物体的密度,而实际情况是物体可以沉入水中说明物体的密度是大于一般的水的密度的,因为ρ物>ρ水时物体下沉。怎么会这样?因为水的密度随着水深度的增加而增加,这和水的压强随着深度的增加而增加是一样的道理,所以水的密度增加意味着水的深度会增加。那么当同样体积的物体的密度(水的体积相同)不同时物体悬浮于水中的深度是不同的,物体密度越大悬浮的深度越深,而当深度超过悬停深度时由于水的密度进一步变大,物体受到的压力就会越大,否则物体就不会悬停了;而在悬停位置以上物体水的密度减小,此时物体的重力及向下的水的压力之和大于水向上的综合力,所以物体继续下沉。可见在物体浸没于水中时关于浮力的公式:ρ水×g×VA(排)中水的密度是变化的,不再是平常的水密度,变化的原因就是当物体浸没入水中时,水的体积增加了,实际情况是水的重量是不变的,而水的密度增大了,所以可以看做是水在物体浸没时增加了和物体一样的重量。那么物体在水中的悬停深度计算如下:
ρ水=ρ物,ρ水={ρ水0×[S×(H1 a)- VA]}/[S×(H1 a) ]=ρ物,令H=H1 a,则:
[ρ水0×(S×H- VA) ]/(S×H )=ρ物,则:
H=(ρ水0×VA)/[(ρ水0-ρ物) ×S];
ρ水0——物体A放入前水的密度,可取平常水的密度。
在本推论中当H1 a>H也就是当物体下沉的深度超过H时就会受到向上的合力,也就是浮力,而且越往下沉受到的浮力越大。
可见文章开头提到的四个试验的结果应该是一致的,导致不一致的原因要不(1)和(4)下沉的深度不够,要么是弹簧计不够灵敏,或许用(2)中增加水体积后的容器来做(1)和(4)的试验且下沉深度合适就会得到不同的结果,减轻铁球和铜球的重量也未必不可。
从上面的推导过程中,可以知道漂浮和悬浮是两个不同的概念。
浮力的定义是:浸在流体内的物体会受到流体竖直向上的作用力。但从上面的推导中我们知道,漂浮在水面的物体受到的综合力是向上的,而浸没悬浮于水中的物体是因为综合力为零才悬浮的,如果综合力不为零那物体要么上浮要么下沉,无法悬浮。可见定义中的浸在流体内的物体的浸在得分两种情况:1.部分浸入;2.全部浸入;其状态就是漂浮和悬浮。
所以应该说物体的浮力是物体可以漂浮在对应流体面上时的固有特性,且物体的浮力与物体的密度和流体的密度有关,与物质的密度无关。漂浮的浮力还具有一定的范围:从完全浮于水面到加载一定重量后物体顶面平于水面的增重量,就像船的承载量一样是同一个道理,只是船为了保证安全不会加载到船舷与水面持平,加载重量后的物体浸入流体内的部分增加,那么相当于深度增加从而导致浮力增加,所以物体受到的浮力在同一种流体中与深度和物体的密度(加载的重量可以看做是物体密度的变化)紧密相关。可见物体的浮力是本身相对于流体具有的,而物体受到的浮力是物体在某种状态下受到流体的作用力,这两者不一定是同一个概念;悬浮于流体中的物体的悬浮深度,与物体的密度和流体的密度有关,但未必与物质的密度有关。
算是补充上一篇文章吧。
,