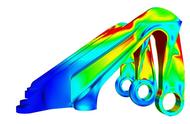
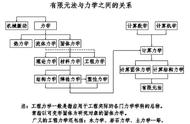
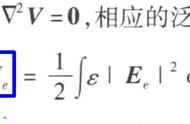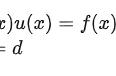以下为笔者目前了解到的几种电磁计算法:
- 传递矩阵法Transfer matrix method(TMM)
- 散射矩阵法 Scattering matrix method(SMM)
- 直线法Method of lines(MOL)
- 严密耦合波法Rigorous coupled‐wave analysis(RCWA)
- 平面波展开法Plane wave expansion method(PWEM)
- 频域有限差分法Finite‐difference frequency‐domain(FDFD)
- 时域有限差分法Finite‐difference time‐domain(FDTD)
- 有限积分法Finite‐Integration‐Technique(FDTD)
- 传输线模型法Transmission line modeling method(TLM)
- 光束传播法Beam propagation method(BPM)
- 部分合并法Slice absorption method(SAM)
- 谱域法Spectral domain method(SDM)
- 边界元法Boundary element method(BEM)
- 间断有限元法Discontinuous Galerkin method(DGM)
- 矩量法Method of moments(MoM)
- 有限元法Finite element method(FEM)
- 积分法计算的是计算整个范围内的所有点,会将完整的矩阵都做推导,不受边界条件限制,是紧密型矩阵;这类算法的网格采用非结构化表面划分网格,主要用于傅里叶空间分析,属于高效半解析型宽带算法,但容易出现收敛性的问题;
- 微分法仅计算局部限定范围的点,只计算临近区域内的矩阵,受边界条件限制,是稀疏型矩阵;这类算法的网格采用结构化体划分网格,主要用于真实空间分析,属于全计算型算法,相对更容易收敛;
在求解时,物体都划分成了很多微小的网格,然后再用不同的算法进行求解。由此我们也可以知道,划分的目的是为了得到一个可靠的结果。这就引出一个概念:收敛性(Convergence)。对于一个要分析的电磁问题,收敛性条件的设置意味着网格划分后麦克斯韦方程是否有确定的解,也意味着此时的求解精度。
简单来讲:这就等同于一个“分辨率”,越高的精度就需要越高的“分辨率”。然而,实际上由于计算机的硬件计算力和存储能力,以及实际工程的精度需求,这个“分辨率”不需要无限的提升,此时收敛性的规格就取决于实际的场景应用了。例如:常规的PCB做分析时,收敛条件只需将Delta S设置成0.02以下即可,而一些天线则需要将Delta S设置成0.01以下,而若要做一些考虑高精度TDR分析,Delta S则需要设置成0.001以下。因此我们要明白:完成了收敛不代表精度就满足了实际场景的需要。原创今日头条:卧龙会IT技术
按精度划分可分为:- 通过收敛性条件将无限个网格描述成有限个网格的微分算法,在多数高精度3D任意结构的全波分析电磁工具里都有用到:FDTD/FDFD/FEM/MOL/ RCWA;
- 已确定电磁场矢量特性的全波积分算法,在多数精度可接受的2.5D层状结构的全波分析电磁工具里都有用到:MoM/BEM/BPM;也有部分3D任意结构的全波分析电磁工具有用到FIT算法;
- TMM传递矩阵法,主要通过矩阵计算传输线导体与介质变化交界处的能量传递,适用于多层介质结构的传输线,分析模型分成任意层来建立;


- BPM光束传播法,主要通过计算平面上的正向能量传输,适用于反射和突变可忽略的结构分析,例如非线性光模块分析;

- MOL直线法,通过将Z方向做解析,X-Y方向做数值计算,以及各导体及介质突变处赋边界条件的半解析半数字化分析法来完成计算,适用于周期性纵向结构的传输线分析;