考试内容:
角的概念的推广.弧度制.
任意角的三角函数.单位圆中的三角函数线.同角三角函数的基本关系式.正弦、余弦的诱导公式.
两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.
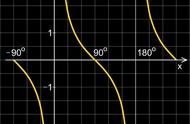
正弦函数、余弦函数的图像和性质.周期函数.函数y=Asin(ωx φ)的图像.正切函数的图像和性质.已知三角函数值求角.
正弦定理.余弦定理.斜三角形解法.
考试要求:
(1)理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算.
(2)掌握任意角的正弦、余弦、正切的定义;了解余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式;了解周期函数与最小正周期的意义.
(3)掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式.
(4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.
(5)理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx φ)的简图,理解A.ω、φ的物理意义.
(6)会由已知三角函数值求角,并会用符号arcsinx\arc-cosx\arctanx表示.
(7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形.
(8)“同角三角函数基本关系式:sin2α cos2α=1,sinα/cosα=tanα,tanα•cosα=1”.
三角函数 知识要点1. ①与α(0°≤α<360°)终边相同的角的集合(角α与角β的终边重合):{β|β=k*360° α,k∈Z}
②终边在x轴上的角的集合: {β|β=k*180°,k∈Z}
③终边在y轴上的角的集合:{β|β=k*180° 90°,k∈Z}
④终边在坐标轴上的角的集合: {β|β=k*90°,k∈Z}
⑤终边在y=x轴上的角的集合:{β|β=k*180° 45°,k∈Z}
⑥终边在轴上y=-x轴上的角的集合:{β|β=k*180°-45°,k∈Z}
⑦若角α与角β的终边关于x轴对称,则角α与角β的关系:α=360°k-β
⑧若角α与角β的终边关于y轴对称,则角α与角β的关系:α=360°k 180°-β
⑨若角α与角β的终边在一条直线上,则角α与角β的关系:α=180°k β
⑩角α与角β的终边互相垂直,则角α与角β的关系:α=360°k β±90°
2. 角度与弧度的互换关系:360°=2π 180°=π 1°=0.01745 1=57.30°=57°18′
注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.
、弧度与角度互换公式: 1rad=180°/π≈57.30°=57°18ˊ. 1°=π/180ι≈0.01745(rad)
3、弧长公式:ι=|α|·r. 扇形面积公式:s扇形=1/2lr=1/2|α|·r²
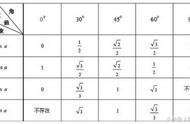
4、三角函数:设α是一个任意角,在α的终边上任取(异于原点的)一点P(x,y)P与原点的距离为r,则sinα=y/r ; cosα=x/r ;tanα=y/x ; cotα=x/y ;secα=r/y ;. .
5、三角函数在各象限的符号:(一全二正弦,三切四余弦)

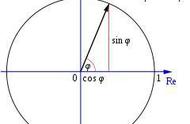
6、三角函数线
正弦线:MP; 余弦线:OM; 正切线: AT.

7. 三角函数的定义域:

8、同角三角函数的基本关系式:sinα/cosα=tanα cosα/sinα=cotα
tan²α cot²α=1 secα·sinα=1 secα·cosα=1
sin²α cos²α=1 sec²α-tan²α=1 csc²α-cot²α=1
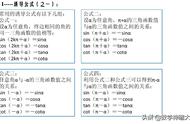
9、诱导公式: