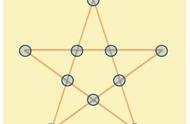
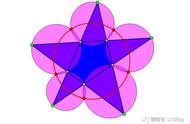
最近,我们在缅怀江泽民同志的同时,也想起他出过的一道数学题“五点共圆”。任意画一个五角星,外面的五个顶点叫做A、B、C、D、E,里面的五个顶点叫做F、G、H、I、J。对外面的五个三角形每一个都做外接圆(即图中五个绿色的圆)。每两个相邻的外接圆会有两个交点,一个靠内,就是五角星的内顶点(即F、G、H、I、J),另一个靠外,是新产生的点(即K、L、M、N、O)。求证:这五个靠外的交点在同一个圆上(即图中那个红色的圆)。你能想到答案吗?

乍一看这道题如此复杂,简直无从下手。实际上,从平面几何关于外接圆的两个基本定理出发,一步一步走,很快就能走通()。
基本的思路是,先证明这五点中的四个点共圆,然后同理得到这五点中的另外四个点也共圆。可见这两个圆是同一个圆,所以这五个点都在同一个圆上。
我们首先要指出,在这里有另一个五点共圆:A、C、N、I、K共圆。仔细看,A和C是五角星的五个外顶点中不相邻的两个,I是五角星的五个内顶点中跟AC相对的那一个,K和N是A和C这两个外顶点的外接圆在朝向I的方向产生的交点。我们要证明,这五个点共圆。
何以见得呢?我们先来证明,这五个点中的四个共圆,就是A、C、I、N这四个点。如果这个能走通,那么根据同样的道理,A、C、I、K这四个点也共圆,所以这两个圆是同一个圆,于是我们就达到了目的:A、C、N、I、K这五个点共圆。
那么,如何证明A、I、N、C四点共圆呢?一个基本的定理是,四点共圆的充分必要条件是,这四个点组成的四边形的对角互补,即加起来等于180度。因此我们要证明:
角ACN 角AIN = 180度。
来看右下方的那个外接圆,N、C、G、H这四个点都属于这个圆,所以:
角GCN 角GHN = 180度。
而角GCN就是角ACN,因为直线AC和直线GC是同一条直线。因此我们要证的就是:
角AIN = 角GHN。
怎么证明这两个角相等呢?来看它们的补角,即180度减去它们。角AIN的补角是角NID,角GHN的补角是角NHD。所以,我们只需要证明这两个补角相等就行了。
而这一点是立刻可以知道的,因为看左下方的那个外接圆,N、D、I、H这四点共圆!回顾一下四点共圆的另一个充分必要条件,这四个点所连成同侧共底的两个三角形的顶角相等。角NID和角NHD,就是这样必定相等的两个顶角。
这样,我们走通了第一步的逻辑链条,证明了A、I、N、C这四点共圆,然后就证明了A、I、N、C、K这五点共圆。
下面我们来走第二步的逻辑链条,即K、L、M、N、O这五点共圆。我们首先来证K、L、M、N这四个点共圆。

为此,我们要证:
角LMN 角LKN = 180度。
何以得知呢?
把角LMN分成两部分,它等于角LMG 角GMN。这两个角各自在一个外接圆里,就容易处理了。下面,我们分别来研究这两部分。
来看右上角的外接圆:
角LMG = 180度 - 角LFG = 角LFA。
再来看上方的外接圆:
角LFA = 角LKA。
由此可见,角LMG = 角LKA。
再来看右下角的外接圆:
角GMN = 角GCN。
而角GCN就是角ACN。然后,我们已经知道五个点A、I、N、C、K共圆,因此:
角GMN = 角ACN = 180度 - 角AKN。
现在仔细看一下,角AKN正是由角LKA和角LKN组成的。因此,我们希望它等于180度的那两个角之和:
角LMN 角LKN = 角LMG 角GMN 角LKN
=角LKA (180度 - 角AKN) 角LKN
=180度。
它确实等于180度。这样,我们就走通了第二步的逻辑链条,K、L、M、N这四点共圆。
剩下一个O点,根据同样的推理,O和其他四点中的任何三个也共圆。
因此最终的结论是,这些圆都是同一个,这五个点共圆。证毕。
最后,我们讲一下关于这道题的小故事。著名数学家张景中院士曾任广东师范学院数学系主任,2000年10月18日,江泽民主席给他打了电话
()。“请问是张景中教授吗?”电话那端的声音似乎有点熟悉。“是,我是张景中。”“你好,我是江泽民。”略微愣了一下,他赶紧回答:“您好,江*。”
原来,是他在《计算机怎样解几何题》书中说,这道题用计算机只要3.9秒就可以完成,然而江泽民感兴趣的是希望知道怎样用人来证明。
江泽民说:“你写的《计算机怎样解几何题》一书,我经常会看看。平时工作太忙,看看这些书可以当作一种很好的休息。我以前也教过职业学校的几何课程,也是个几何爱好者。那本书里有些我不明白的想请教你。”接着江泽民将题目一字不漏地说了出来,“你能否把证法写给我呢?”“可以。”随后,江泽民还对张景中的经历和现在从事的智能教育软件研究开发工作表示了极大的关心。
就在这次谈话后两个月,2000年12月20日,江泽民到澳门出席澳门特别行政区成立一周年庆祝活动,把这道题出给了澳门的中学生。当时,没有人能现场给出答案。江泽民笑着告诉大家,自己也是向广东一位老师请教以后才找到答案的。他说:“我把这道题出给濠江中学是要说明:一个人要有钻研精神。”江泽民离开澳门后,一些老师还将解法寄到北京。江泽民亲笔复信,对澳门老师表达谢意,并鼓励他们为澳门培养出更多的优秀人才。
,