如果你随手画一个五角星(不一定是正五角星),再作出这个五角星的五个角上的三角形的外接圆,这五个圆除了在五角星上的那五个交点外,在五角星外面还有另五个交点。有趣的是,不管五角星是什么样,后五个交点一定在同一个圆上。这就是五圆定理。
五圆定理
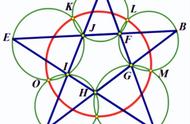
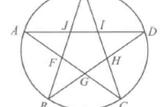
如下图所示。随意画一个五角星。设五角星的五个顶点分别为A、B、C、D、E。五角星五条边之间互相交出五个点为F、G、H、I、J,构成一个五边形。五个顶点与五边形的五条边分别构成五个三角形。分别作这五个三角形的外接圆,所作出的这五个圆中每两个相邻的圆之间又交出一个除三角形顶点以外的另一个点,这样得到的点有五个(图中分别为K、L、M、N、O)。那么,这五个点共圆。

(1)先证C、E、K、F四点共圆。因为A、F、J、K四点共圆,所以有
∠AFK = ∠AJK(图中深蓝色的角)
(理由:等弧上的圆周角相等)
又因为I、J、K、E四点共圆,所以有
∠AJK=∠IEK
(理由:圆内接四边形一个角的外角等于它的对角)
所以
∠AFK=∠IEK
所以C、E、K、F四点共圆
(理由:四边形CEKF一个角的外角等于它的对角,则四边形为圆内接四边形)
(2)同理可证C、M、F、E四点共圆(观察图中粉红色角)。
(3)由上面的(1)和(2)得知,
C、E、K、M四点共圆,
即四边形CEKM为圆内接四边形
(4)由上面的(3)知,在四边形CEKM的对角之和等于180度,我们考虑下面这组对角之和:
∠CMK ∠KEI = 180°
而
∠CMK=∠NMK ∠CMN(红色角)
∠KEI = ∠KOI(蓝色角)
把上面两式代入上上式,得
∠NMK ∠CMN ∠KOI = 180°
又因为
∠CMN = ∠CHN = ∠NOI(红色角)
所以有
∠NMK ∠NOI KOI= 180°
即
∠NMK (∠NOI KOI) = 180°
∠NMK ∠NOK = 180°
所以M、N、O、K四点共圆。同理可以证明N、O、K、L四点共圆。这两组四点中都包含N、O、K三点,而过三点的圆是唯一的。所以有
M、N、O、K、L五点共圆
证毕
有关这个定理,张景中院士在他的著作《计算机怎么解几何题——谈谈自动推理》中有过很深入的阐述。他说不光这五个点共圆,另外还有两个都由五个点构成的点组,一共十个点也在这个圆上,即十五点共圆!

有关五圆定理,还有过一段很有意思的佳话。这里就不多说了,有兴趣的您可以上网搜索。
文章来源:搜狐网,2017年。
更多资料可以查询百度百科的词条:密克定理。
以下内容来自百度百科。
密克定理是几何学中关于相交圆的定理。1838年,奥古斯特·密克(Auguste Miquel)叙述并证明了数条相关定理。许多有用的定理可由其推出。
定理:设在一个三角形的每一边上取一点,过三角形的每一顶点与两条邻边上所取的点作圆,则这三个圆共点[2]。利用圆周角性质易证此定理。
1838年奥古斯特·密克在约瑟夫·刘维尔的期刊《Journal de mathématiques pures et appliquées》(纯粹与应用数学杂志)发表了这定理的一部份。
密克的第一条定理,是十八世纪已有的著名经典结果,以圆周角定理证明。
完全四线形四圆的交点称为密克点,但这性质雅各布·施泰纳在1828年已经知道,威廉·华莱士也已经知道。
五圆定理是一条更一般的定理的特殊情形。这条定理由威廉·金登·克利福德提出及证明。
科学尚未普及,媒体还需努力。感谢阅读,再见。
,