上到菲波那契数列,下到我们常见的五角星,竟然都暗含黄金分割,这就是数学之美。
1五角星图形我国的国旗、国徽、军旗、军徽都采用了五角星图案(一些其他国家也是如此)。而发现黄金矩形的毕达哥拉斯学派的会徽也是一个五角星,每个会员都佩带一个五角星标记的徽章。为什么五角星会成为众多民族喜爱的图形?正五角星图形到底具有哪些美感呢?
五角星的形成来自于大自然(如五角星形花瓣),它也和大自然一样,既有美妙的对称也有扣人心弦的变化。
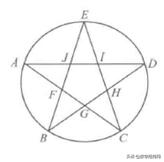
图1
将圆周分成五等分,依次隔一个分点相连,则可一笔画成一个图形,即成一个正五角星形(如图1)。首先,在连接的过程中就让人惊异于形成图形的奇妙(奇异的美);而连成的图形又具有如此明显的对称性(对称的美)!五角星美的核心是五条边相互分割成黄金比(如图中F、G是AC的黄金分割点),这是一种最匀称的比,能给人产生美的原动力。
因此,五角星形具有如此巨大的魅力,成为世人所喜爱的图形。
2黄金图形请看下面的几种黄金图形。
黄金矩形:宽与长之比为黄金数的矩形。对黄金矩形依次舍去所作的正方形,可得到不断缩小的黄金矩形序列(如图2)。
黄金三角形:分两类,第一类是底与腰之比为黄金数的三角形,如图3中的△ABC,△BCD,△DEC,……组成不断缩小的三角形序列;第二类是腰与底之比是黄金数的三角形,如图4中的△ABC,△DAB,△EBD,……也组成不断缩小的黄金三角形序列,前述的埃及胡夫金字塔,其正投影即为此类黄金三角形。

图2

图3
黄金椭圆:短轴与长轴之比为黄金数的椭圆(如图5)。它的面积与以它的焦距为直径的圆的面积相等:它的离心率的平方也是黄金数。
黄金双曲线:实半轴与半焦距之比为黄金数的双曲线(如图6)。它的离心率的倒数也是黄金数。
这些黄金图形使人看起来赏心悦目,是同类图形中最和谐、优美的图形。