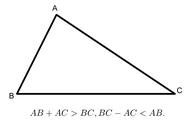
三角形的任意两边之和大于第三边;任意两边之差小于第三边.
注意:(1)三边关系的依据是:两点之间线段是短;
(2)围成三角形的条件是任意两边之和大于第三边.
7
三角形的角与角之间的关系
(1)三角形三个内角的和等于180°;
(2)三角形的一个外角等于和它不相邻的两个内角的和;
(3)三角形的一个外角大于任何一个和它不相邻的内角.
(4)直角三角形的两个锐角互余.
8
三角形的内角和定理
定理:三角形的内角和等于180°.
推论:直角三角形的两个锐角互余。
推理过程:
(1)作CM∥AB,则∠4=∠1,而∠2 ∠3 ∠4=180度,
即∠A ∠B ∠ACB=180度.
(2)作MN∥BC,则∠2=∠B,∠3=∠C,而∠1 ∠2 ∠3=180度
即∠BAC ∠B ∠C=180度.

注意:
(1)证明的思路很多,基本思想是组成平角.
(2)应用内角和定理可解决已知二个角求第三个角或已知三角关系求三个角.
9
三角形的外角的定义
三角形一边与另一边的延长线组成的角,叫做三角形的外角.
注意:每个顶点处都有两个外角,但这两个外角是对顶角.(所以一般我们只研究一个)
如:∠ACD、∠BCE都是△ABC的外角,且∠ACD=∠BCE.
所以说一个三角形有六个外角,但我们每个一个顶点处
只选一个外角,这样三角形的外角就只有三个了.
10
三角形外角的性质
(1)三角形的一个外角等于它不相邻的两个内角之和.
(2)三角形的一个角大于与它不相邻的任何一个内角.

注意:(1)它不相邻的内角不容忽视;
(1)作CM∥AB由于B、C、D共线
∴∠A=∠1,∠B=∠2.
即∠ACD=∠1 ∠2=∠A ∠B.
那么∠ACD>∠A.∠ACD>∠B.
11
三角形的稳定性
三角形的三边长确定,则三角形的形状就唯一确定,这叫做三角形的稳定性。
注意:(1)三角形具有稳定性;
(2)四边形没有稳定性.
关于三角形会经常遇到的题型:
适当添加辅助线,寻找基本图形。
(1)基本图形一,如图8,在ABC中,AB=AC,B,A,D成一条直线,