三角函数题型多但有规律。
三角函数这一模块的特点就是题型多,但是题型比较固定,只要大家学一定是能学懂的。
以前三角函数都怎么学的?初中阶段把这个角放在直角三角形里面,规定是死规定,这个角的对边比斜边是它的science,零边比斜边是它的cos,指它的对边比零边是它的摊着的值。
这定义有什么不好的地方?
·第一,笔直关系是死规定,有什么实际意义?好像没体现出来。
·第二,更明显的缺陷,把好的一个角放在直角三角形里面,这个角肯定是一个锐角。换句话说,以前只会求一个锐角的三角函数,但是现在知道角度可以是任意取值的,一百二十度、三百五十度、九百六十度还能放锐角三角形里吗?就不能了。所以以前这种定义需要摒弃掉,需要把它进行升级。

今天第一个任务就是学习任意角度的三角函数的新定义。在任意角那些视频里面讲过,角度有始边有终边,任何一个角都有唯一确定的一条终边。
现在在平面直角做游戏里面以圆点为圆心画一个圆,圆的半径是一,这很重要,半径是一,这是一,这是一,这也是一,半径为一的圆称之为单位圆。

惊奇的发现这角不是有一个中边吗?这中边跟单位圆有且仅有一个焦点对不对?把坐标设为x零y零,每个角都有个中边,每个中边都跟单位圆有切仅有一个焦点。数学家就开始发挥想象力了,得把焦点的坐标利用起来。
数学家们规定焦点的横坐标就是这个角的cosine值,看好了横坐标在哪?做个垂线下来,这就是这个点的横坐标表,记为cosinealpha这点的纵坐标,这一段即为sinealpha。最后把纵坐标比横坐标,笔直即为tangent而发。

这就是在高中阶段对三角函数的全新定义。肯定有宝贝有很多疑问。
·第一,新定义跟以前的定义冲不冲突?答案是不冲突的。知道竖直长度是动作标y零,水平长度是横坐标x0,而且非常关键的半径因为是单位圆,半径的长度永远是一,所以即便是按照以前锐角三角函数的定义放在直角三角形里面。
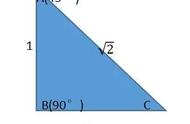
什么是三亚阿尔法?就是对边比斜边,对边比斜边y零比一,还是y零吗?类似的。现在想求cosanalpha,cosanalpha怎么求零边比斜边?不就是x0比一吗?x零比一不就是x0吗?摊着的就更是了,想就摊着那,让对边比零边,不就y零比x0吗?所以新定义是包含原有定义的基础上更高级的定义。因为它不仅能求锐角的三角函数,甚至能求一个钝角。在这个定义之下钝角随便举个例子,它也是有三角函数的,一百三十五度,塞扣塞他人都是几?来试着做一做。