特点分析:
利用等边三角形的性质,可以灵活地解决一些共顶点等边三角形问题. 解决这类问题常用的方法是:利用等量减等量所得的差相等,得到共顶点处的一组角相等,再通过“SAS”证明两个三角形全等解决问题.
问题原型:
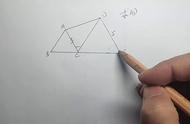
如图1,△ABD和△AEC都是等边三角形. 求证:DC = BE.

分析: 利用等边三角形的每一个内角都为60°,得公共顶点A处的∠DAC = ∠BAE,再利用等边三角形的各边都相等,根据“SAS”证明△DAC ≌ △BAE即可.
证明: 在等边三角形ABD中,AD = AB,∠DAB = 60°,
在等边三角形AEC中,AC = AE,∠EAC = 60°,
所以∠DAB = ∠EAC.
因为∠DAC = ∠DAB ∠BAC,∠BAE = ∠EAC ∠BAC,
所以∠DAC = ∠BAE.
在△DAC和△BAE中,AD=AB,∠DAC=∠BAE,AC=AE,
所以△DAC ≌ △BAE(SAS). 所以DC = BE.
模型应用:
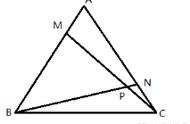
如图2,△ABC和△BDE均为等边三角形,点E在线段AD上. 求证:BD CD = AD.

分析: 等边三角形ABC和等边三角形BDE的公共顶点为点B,易得∠ABE = ∠CBD,先根据“SAS”证得△ABE ≌ △CBD,可得AE = CD,再利用AD = AE DE,通过等量代换即可.
证明: 因为△ABC和△BDE均为等边三角形,
所以∠ABC = ∠DBE = 60°,AB = BC,BE = BD = DE.
所以∠ABC - ∠CBE = ∠DBE - ∠CBE,即∠ABE = ∠CBD.
在△ABE和△CBD中,AB=CB,∠ABE=∠DBC,BE=BD,
所以△ABE ≌ △CBD(SAS). 所以AE = CD.
因为AD = AE DE,BD = DE,
所以AD = CD BD.
应用练习:
如图3,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE = BD. 求证:△ADE为等边三角形.

(提示:先通过“SAS”证得具有公共顶点的△ABD ≌ △ACE,得到AD = AE,∠BAD = ∠CAE,再证∠DAE = 60°即可.)
解:因为△ABC为等边三角形,所以∠B = ∠ACB = 60°.
所以∠ACD = 120°.
因为CE平分∠ACD,所以∠ACE = 60°.
在△ABD和△ACE中,AB=AC,∠B=∠ACE,BD=CE,
所以△ABD ≌ △ACE(SAS).
所以AD = AE,∠BAD = ∠CAE.
因为∠BAC = ∠BAD - ∠CAD = 60°,
所以∠DAE = ∠CAE - ∠CAD = 60°.
所以△ADE为等边三角形.