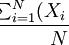- 小方差 - 数据点往往非常接近均值且彼此非常接近
- 高方差 - 数据点与均值和彼此之间非常分散
- 零方差——所有数据值都相同
标准偏差是数据集中的平均变异量。 它平均表示每个数据点与平均值相差多远。标准差越大,数据集的可变性越大。

当拥有总体数据时可以获得总体标准差的准确值。 可以从每个总体成员收集数据,因此标准差反映了分布(总体)中的精确变异量。
但当无法获得所有数据时,就可以对整体数据进行抽样(抽样方式这就不详细介绍)。抽样的结果就被称作样本,样本的作用是对总体的数据进行统计推断的。当使用样本数据时,样本标准差始终用作总体标准差的估计值。 在这个公式中使用 n 往往会给你一个有偏差的估计,它总会低估可变性。
将样本 n 减少到 n - 1 会使标准偏差人为地变大,从而提供对变异性的保守估计。虽然这不是无偏估计,但它是对标准差的偏少估计:高估而不是低估样本的可变性更好。

标准差低 - 数据点往往接近平均值 标准差高 - 数据点分布在大极差的值上
什么是变异性的最佳衡量标准?可变性的最佳衡量标准取决于不同衡量标准和分布水平。
对于在序数水平上测量的数据,极差和四分位距是唯一合适的变异性度量。
对于更复杂的区间和比率的数据,标准差和方差也适用。
对于正态分布,可以使用所有度量。 但标准差和方差是首选,因为它们考虑了整个数据集,但这也意味着它们很容易受到异常值的影响。
对于偏态分布或具有异常值的数据集,四分位距是最好的度量。 它受极值影响最小,因为它侧重于数据集中间的部分。
作者;Ashish Kumar Singh
,