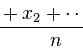实际生活中,人们除了关心数据的“平均水平”外,往往还关心数据的离散程度,即它们相对于“平均水平”
的偏离程度也叫数据的离散程度,极差、方差(标准差)是刻画数据离散程度的统计量。
一、数据离散程度统计量:
1、极差:
一组数据中的最大数据与最小数据的差叫做这组数据的极差。
极差反映的是一组数据的 变化范围 ,极差 = 最大值 - 最小值。
2、方差:
①设有n 个数据x1,x2,…,xn ,各数据与它们的平均数的差的平方分别是 :

图(1)
我们用它们的平均数,即用:

图(2)
来衡量这组数据的波动大小,并把它叫做这组数据的方差(variance),记作s^2 ,
方差的算数平方根叫做标准差,记作 s 。
②方差是刻画数据的波动程度,方差越大,数据的波动越大;方差越小,数据的波动就越小。
③用样本估计总体是统计的基本思想,正像用样本的平均数估计总体的平均数,考察总体方差时,如果所要考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常是用样本的方差来估计总体的方差。
二、典型例题:
1、极差: