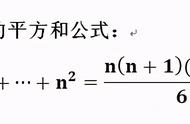求三角形的角度
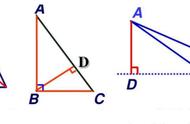
三角形ABC中∠ABC=45°, D在BC上,且CD=2BD,∠DAB=15°,求∠ACB大小。

解法1: 如图在AD上取DE=DC, 由于∠ADE=∠CAB ∠DBA=15° 45°=60°

所以△CED为正三角形,取F为ED中点, 连接BF,由于FD=CD/2=BD,
由于∠CDF=∠DAB ∠DBC=15° 45°=60°
因此∠DBA=30°,所以∠FBA=15°,因此AF=BF,即∠FBA=15°
所以∠FCB=90°-60°=30°
而 FBC=45°-15°=30°
所以BF=CF
故AF=CF
∠ACF=45°
因此∠ACB=45° 30°=75°
解法2:如题,直接做AD的高

显然DE=AD/2, 因此DE=DB,
∠DEB=∠DBE=30°
所以∠EBA=45°-30°=15°=EAB
故EA=EB,
另外∠EBC=∠ECB=30°
所以EC=EB
因此EA=EC
故∠ACE=45°
所以∠ACB=45° 30°=75°
,