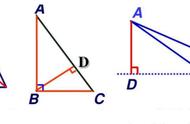
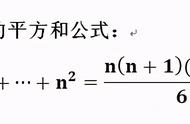如图,任意的一个△DEF的面积可以以边EF为底,高就是DH,所以S[△DEF]=(1/2)EF•DH,这个在小学阶段就已经掌握,那么在求一个三角形面积中,底和高可不可以突破限制呢?

其实在求三角形面积时,底和高没有任何限制,如下图可以表示成(1/2)DK•EG,注意这边K是直线EF上的任意一点,当K在边EF上时,DK把△DEF的面积分成两部分,S[△DEF]=S[△DEK] S[△DFK]
S[△DEF]=(1/2)DK•EQ (1/2)DK•FM=(1/2)DK•(EQ FM),显然MQGF是矩形,MF=QG
∴ S[△DEF]=(1/2)DK•(EQ FM)=(1/2)DK•(EQ QG)=(1/2)DK•EG

(1)如果点K在边EF的延长线上,如上图所示,通过推导可以算出此时S[△DEF]=(1/2)DK•EL

(2)如果点K在边EF的延长线上,如上图所示,通过推导可以算出此时S[△DEF]=(1/2)DK•ER