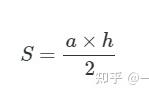怎样想到用三角形面积公式?

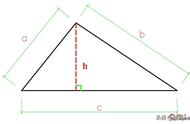
初看这个问题,感觉很无聊,求三角形面积,不用公式用什么?但随着教学推进过程中越来越多地出现了应该使用面积公式,学生即始终想不到用它,于是返回来重新审视这一应用最为广泛的面积公式,三角形的面积等于底与高乘积的一半,应该不简单。
最初级的应用就是给出三角形的底和高,计算三角形的面积,使用到的运算为乘法,现在在运算上提升,已知面积求底,或求高,立刻转变为除法,再变下去,只是简单增加运算量,并不值得。
换个方式考察,融入观察图形,这次应用起来十分精彩,以下面两道试题为例。
第一题
如图,△ABC的面积为4cm²,AP与∠ABC的平分线垂直,垂足为P,则△PBC的面积为__________cm².

解析:
条件元素有△ABC的面积,BP平分∠ABC,AP⊥BP,所求结论是△PBC的面积;
由△ABC的面积出发,求△PBC的面积,并且题目其它条件并无一个关于线段长度,意味着用最初级的面积公式法不可行,因此我们必须寻找这两个三角形面积之间的数量关系,并且由于△PBC在△ABC内部且共边,猜测它们是倍数关系,下面来证实。
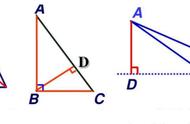
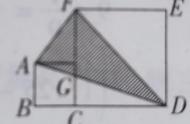
BP是角平分线,同时也是AP的垂线,这两种性质的线重合,极易联想到等腰三角形中的“三线合一”,那么,等腰三角形在哪里呢?不妨延长AP交BC于点D,如下图:

我们很容易证明△ABP和△DBP中,∠BAD=∠BDA,于是BA=BD,得到等腰△ABD,然后根据三线合一,得到点P为AD中点;
至此本题的钥匙拿到了,BP是△ABD的中线,CP是△ACD的中线,它们都可以将三角形分成面积相等的两部分,于是S1=S2,S3=S4,而这四部分之和为4cm²,所以“各取一半”得到S2 S4=2,所以△PBC的面积为2cm²;