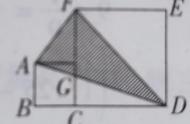
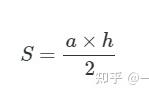从本题思维导图可以看出,AC=2BC其实是个伏笔,触发方程的关键结论是△ABC的面积,仍然与上一题类似,从面积得到面积,并且△A'B'C'与△A'B'C同底,且高存在3倍的数量关系,而这个数量关系要想能观察出来,又必须延长DC得到整个△A'B'C'的高,平行线的关系也要能从轴对称中推导出来,因此本题难度实际上在于找到各条件元素间的关联,找不到,便会跟老师说看不懂题目。
解题反思
这两道与三角形面积有关的填空题,学生刚刚上手的时候,多数有点懵,不知从哪突破,也就是说,轴对称的本质含义并未深入理解,更没想到三角形面积公式在这两道题中的使用。
我们返回到课堂教学中,三角形面积计算公式,学生真的理解了吗?
求三角形的面积,小学生也知道是底乘以高再除以2,如果我们在教学中始终给出底和高来求面积,属于机械重复,达不到深入理解这个公式的目的,在初中阶段,对它的运用更为灵活,底和高未必会直接从图中反映出来,缺底或缺高的情况比比皆是,这种结构不良类的习题,更考验学生的整体建构能力,如何才能让学生想到,是我们在教学过程中孜孜以求的大成之境。
以三角形面积计算公式为例,首先要站在整个初中学段角度去看待它,在学习三角形、四边形、平移、轴对称、旋转等章节的过程中,从不同角度去考查学生对公式的理解;其次是在每一次解题过程中,如果因为没有想到使用它,一定在要反思中点明,尤其是在对学生分析解题思路的时候,说清为什么要这么想,引导学生多问“为什么”,最后在学生解题过程中,有意识地弥补他们的知识体系里的漏洞,通过提示也行,反思也罢,这个环节不可少。
当然,这一切的前提,是作为教师要多研题,去挖掘试题背后的知识框架,思考怎样让学生也建立起对应的框架。
*爱数学做数学
,