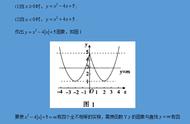
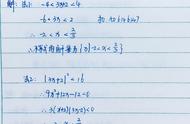有理数五大类型拔高题专项练习二:分段解析及最值规律。
答案会在第二天评论栏发布(置顶),敬请关注。[玫瑰][玫瑰][玫瑰][玫瑰]

本次重点练习绝对值的分段解析练习,总结绝对值加减规律及最值计算方法。(找绝对值的“0”点分段解析)
1、当x<3、5≥x≥3时、x>5时,化简|x-3| |x-5|。
2、分段化简||x-1|x-2| |x 1|。(找“中点”和“0”点分段点的关系)
3、当|x-2| |x 2|=4时,求x的取值范围。
4、求|x-1| |x-2|的最小值。
5、求|x-1| |x-2| |x-3|的最小值及x的取值。(总结规律)
6、求|x-1| |x-2| |x-3| |x-4| |x-5|的最小值及x的取值。(总结规律)
7、求|x-1| |x-2| |x-3| |x-4| |x-5| |x-6|的最小值及x的取值范围。(总结规律)
8、|x-1| |x-2| …… |x-2020|的最小值时x的取值。
9、|x-1| |x-2| …… |x-2021|的最小值时x的取值。
10、求3|x-1| |x-2|的最小值。(总结规律)
11、求2|x-1| 5|x-2|的最小值。(总结规律)
12、求|x-1|-|x-2|的最值(最大值和最小值)。
13、求m|x-1|-m|x-2|的最值(最大值和最小值)。
14、求|x-2| |x 4| |x-6|的最小值及x的取值。
15、求|3x-2| |2x 4| |4x-6|的最小值及x的取值。
16、求|⅓·x-2| |½·x 4| |¼·x-6|的最小值及x的取值。
17、当|x-1| |x-2|为最小值时,|x-1| |x-2|-|x-3|的最大值和最小值。
18、已知|x 2| |x-2|=10-|y 3|-|y-3|,求x y的最大值和最小值。
19、|x-4|=4-x,求x的取值范围。
20、|2x-1|≤1,求x 的取值范围。