结合工程实际,介绍了椭圆旋转楼梯的微分几何数学模型,阐述了楼梯施工放样的基本方法,即根据已知两端点的参数,进行椭圆弧长等分。
椭圆弧长积分结果无法用解析解显式表示 ,利用泰勒级数推导出弧长积分的近似解析解,然后利用 New2 ton迭代法手算各弧长等分点对应的参数 t,从而求出椭圆旋转楼梯各控制点的坐标。
同时利用 Matlab软件编程计算进行校验。比较手算和机算结果,发现该解析解完全满足工程设计要求。
这种方法还可以用于以其他方式旋转楼梯的施工放样。
1
.概述
椭圆只有两条对称轴 ,弧上每点曲率均在变化 , 弧长积分无法用简单的解析函数表达。椭圆等距线并不是椭圆 ,椭圆产生椭圆螺旋线、直纹曲面均给计算带来很大难度。因此 ,椭圆螺旋楼梯的施工放样和内力分析是个相当复杂的过程 ,国内外相关研究较少[ 1 - 3 ] 。
20世纪 80年代末国际知名建筑大师丹下健三曾在约旦哈西姆宫的 5 个不同使用功能的大厅里 , 设计了 5种不同的椭圆旋转楼梯。本文以其中某一会客厅内的椭圆螺旋楼梯为工程背景。
该椭圆旋转楼梯中心线的水平投影为椭圆 ,其长半轴为 4. 2 m, 短半轴 2. 4 m;梯宽 1. 2 m,内边线与外边线的水平 投影为两条与椭圆中心线相距 0. 6 m 的椭圆等距线。踏步按照弧长等分进行定位。楼梯右向旋转。旋转一周上升高度为 10. 2 m。利用微分几何方程建立楼梯的数学模型之后 ,便可根据弧长等分进行精确的施工放样。鉴于当时计算机尚未普及 ,推导出椭圆弧长近似积分公式 ,然后利用该公式进行放样计算。
同时文中还利用 Matlab软件编程计算并比较 ,结果表明该公式的精确程度完全满足工程要求。
2
.椭圆螺旋楼梯的数学模型
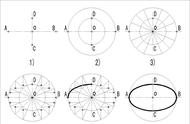
将休息平台简化为连续梯段的一部分。直纹曲面 S ∶r( t, v) 由两个参数 t和 v控制。给定参数 v, 可以得到一组 t线 , 楼梯的中心曲线、内外边线包含在这些 t线中 : v = 0时即为中心线椭圆螺旋线 LR , 楼梯的内外边线则分别是中心曲线 LR 在主矢方向上的等距线 LR·E ( v0 分别为 600、- 600) 。给定参数 t则可得到一组 v线 , v线是一组平行于 x0y平面的直线 , 方向正好为椭圆螺线的法线方向 , 因此 , 楼梯踏步的边线就属于 v线 [ 4 ] 。
如图 1所示。t线和 v线是直纹面上的两组正交曲线。整个椭圆旋转楼梯分布在光滑连续的空间直纹曲面上。椭圆旋转楼梯中心曲线椭圆螺旋线 LR 在 x0y平面上的投影为椭圆曲线 r( t) 。如椭圆螺旋楼梯模型图 1所示 , 各参数方程等见表 1。


3
.椭圆弧长计算公司的近似解析
由上述分析可知椭圆弧长

式中 :ρ = ( a sin t) 2 ( bcost) 2 , 称为椭圆弧长的导数。椭圆弧长属于第二类勒让德 (Legendre) 椭圆积分 , 积分结果无法用解析解显式表示 [ 5 ] 。
椭圆楼梯施工放样和力学分析时将进行 t和 l ( t) 之间的互逆运算。求解椭圆弧长 l ( t) 关于参数 t的解析表达式 , 既可以进行手算 , 同时可以与机算结果互相校 核。利用 1 x2 在其收敛半径 | x | ≤ 1内的二项级数展开式 , 将椭圆弧长积分展开为级数表达式 , 从而求出椭圆弧长的近似解析解 :