点击右上角关注“陈老师初中数理化”分享学习经验,一起畅游快乐的学习生活。
在平面直角坐标系求解满足条件的点坐标是初中数学的重要题型,本文就例题详细解析这类题型的解题思路,希望能给初中学生的数学学习带来帮助。
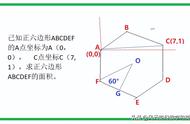
例题如图,正六边形ABCDEF的边长为2√3,延长BA,EF交于点O,以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,求直线DF与直线AE的交点坐标。

解题过程:
延长DE交y轴于点G,过点F作FM⊥x轴于点M

根据根据正六边形的性质和题目中的条件:正六边形ABCDEF的边长为2√3,∠EFA=∠FAB=∠DEF=120°,AB=BC=CD=DE=EF=AF=2√3;
根据结论:∠EFA=∠FAB=∠DEF=120°,则∠OFA=∠OAF=∠GEO=60°;
根据结论:∠OFA=∠OAF=60°,则△OFA为等边三角形;
根据等边三角形的性质和结论:△OFA为等边三角形,AF=2√3,则OF=AF=OA=2√3,∠AOF=60°;
根据结论:x轴⊥y轴,∠AOF=60°,则∠EOG=30°;
根据结论:∠EOG=30°,∠GEO=60°,则∠EGO=90°,即DG⊥y轴;
根据结论:OF=EF=2√3,则OE=OF EF=4√3;
根据直角三角形性质和结论:DG⊥y轴,∠EOG=30°,OE=4√3,则GE=OE/2=2√3;
根据勾股定理和结论:DG⊥y轴,OE=4√3,GE=2√3,则OG=6;
根据结论:GE=2√3,DE=2√3,则DG=DE GE=4√3;
根据三线合一性质和结论:△OFA为等边三角形,FM⊥OA,OA=2√3,则OM=OA/2=√3;
根据结论:DG=4√3,OG=6,GE=2√3,OA=2√3,则点D的坐标为(4√3,6),点E的坐标为(2√3,6),点A的坐标为(2√3,0);
根据勾股定理和结论:FM⊥x轴,OF=2√3,OM=√3,则FM=3;
根据结论:OM=√3,FM=3,则点F的坐标为(√3,3);
设直线DF的解析式为y=kx b
根据结论:直线DF:y=kx b经过点D、F,D(4√3,6),F(√3,3),则k=√3/3,b=2;
所以,直线DF的解析式为y=√3/3x 2;
根据结论:A(2√3,0),E(2√3,6),则直线AE的解析式为x=2√3;
根据结论:直线DF:y=√3/3x 2,直线AE:x=2√3,则交点坐标为(2√3,4)。
结语解决本题的关键是利用正六边形的边长、角度,合理添加辅助线构造出等边三角形、直角三角形,得到线段间的数量关系,再根据点坐标与线段长度间的关系,就可以求得直线上的点坐标,进而求得一次函数解析式和交点坐标。
,